تدریس فصل اول حسابان دوازدهم (تابع)

رسم نمودار توابع به کمک نمودار توابع دیگر

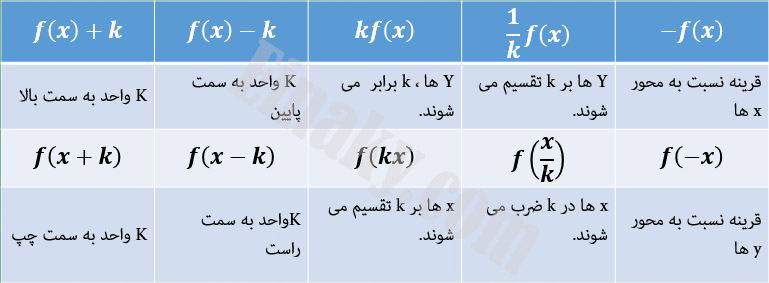
اگر نمودار تابع f(x)=y را داشته باشیم و k عددی مثبت باشد، در این صورت نمودار توابعی که به کمک (f(x به دست می آید مشابه زیر است:

•  اگر k>1 باشد، نمودار تابع f(x)=y از انبساط عمودی و اگر k بین صفر و یک باشد نمودار f(x)=y از انقباض عمودی در راستای محور y ها به دست می آید.
•  اگر k>1 باشد، نمودار تابع f(x)=y از  انقباض افقی و اگر k بین صفر و یک باشد نمودار f(x)=y از انبساط افقی در راستای محور x ها به دست می آید.

نکته:
برای رسم نمودار |(y=|f(x ابتدا نمودار f(x)=y را رسم  می کنیم.

سپس بخش هایی از نمودار که زیر محور x ها قرار دارد را، نسبت به همین محور قرینه می کنیم.

نکته:
برای رسم نمودار |(y=|f(x ابتدا نمودار f(x)=y را رسم می کنیم.

سپس بخش هایی از نمودار که در سمت چپ محور y ها قرار دارد را، حذف کرده  و به جای آن قرینه آن قسمت از نمودار f که در سمت راست محور y ها واقع است را در سمت  چپ محور y ها نیز رسم می کنیم.

در واقع نمودار |(y=|f(x نسبت به محور y ها متقارن باشد.

اگر n یک عدد صحیح نامنفی و a₀,a₁,a₂,a₃,…a_n اعداد حقیقی باشند، که a₀≠0 در این صورت به تابع f با ضابطه زیر یک تابع چند جمله ای از درجه n می گویند.

f(x)=a_n xⁿ+a_(n-1) x^(n-1)+…a₂ x²+a₁ x +a⁰

تابع درجه سوم

اگر a≠0  به تابع چند جمله ای با ضابطه

f(x)=ax³+bx²+cx+d

تابع درجه سوم گفته می شود. ضابطه ساده ترین تابع درجه سوم، به صورت f(x)=x³  است.

نکته:
تابع f روی بازه I اکیدا صعودی است هر گاه:

(x₁<x₂,f(x₁ )<f(x₂

تابع f روی بازه I اکیدا نزولی است هر گاه:

(x₁<x₂,f(x₂ )<f(x₁

تابع f روی بازه I صعودی است هر گاه:

(x₁<x₂,f(x₁ )<f(x₂

تابع f روی بازه I نزولی است هر گاه:

(x₁<x₂,f(x₂ )<f(x₁

قضیه تقسیم برای چند جمله ای ها

اگر (f(x و (p(x توابع چند جمله ای باشند و درجه (p(x  از صفر بزرگ تر باشد، آنگاه توابع چند جمله ای منحصر به فرد (q(x و (r(x وجود دارند که در آن درجه (r(x از درجه (q(x کمتر است.

(f(x)=p(x)q(x)+r(x

نکته: اگر در قضیه تقسیم، درجه (f(x برابر n و درجه (p(x برابر m باشد، آنگاه درجه (q(x برابر n-m و درجه (r(x حداکثر برابر m-1 خواهد بود.

 نکته: در قضیه تقسیم  اگر r(x)=0 باشد ، آنگاه تابع f بر تابع  p بخش پذیر است و در این صورت داریم:

(f(x)=p(x)q(x

در این صورت به (p(x  و (q(x عامل یا فاکتور (f(x می گویند.

نکته:
اگر در قضیه تقسیم داشته باشیم r=f(-b/a)=0   آنگاه چند جمله ای (f(x بر ax+b بخش پذیر است.

در این حالت به ax+b فاکتور یا عامل (f(x نیز گفته می شود.

نکته:

تعبیر هندسی حالتی که چند جمله ای (f(x بر ax+b بخش پذیر است، این است که نمودار چند جمله ای (f(x محور x ها را در نقطه ای به طول(b/a-) قطع می کند.

روش تعیین باقی مانده تقسیم وقتی درجه مقسوم علیه بیشتر از 1 است.

برای یافتن باقی مانده چند جمله ای (f(x بر چند جمله ای (p(x وقتی درجه (p(x برابر با یک نباشد، ابتدا (p(x  را برابر با صفر قرار می دهیم و رابطه ای که به دست می آید را در مقسوم علیه قرار می دهیم.

این عمل را تاجایی ادامه می دهیم که درجه مقسوم از درجه مقسوم علیه کمتر شود.

توجه کنید که وقتی درجه مقسوم علیه بزرگتر از یک باشد، برای یافتن باقی مانده هرگز ریشه مقسوم علیه (در صورتی که دارای ریشه باشد ) را نباید به دست آورد.