تدریس فصل دوم حسابان دوازدهم (مثلثات)

یادآوری و تکمیل اتحاد های مثلثاتی

فرمول های مهم  مثلثاتی

توابع متناوب و دوره تناوب

تابع متناوب: تابع f را  متناوب می گوییم، هر گاه عدد حقیقی غیر صفر c موجود باشد که اولاً برای هر x عضو دامنه f، مقدار x±c نیز متعلق به دامنه تابع f باشد و ثانیاً

 (f(x±c)=f(x

به عدد c دوره تناوب تابع f می گوییم.

دوره تناوب اصلی: به کوچکترین عدد حقیقی و مثبت C که در تعریف فوق صدق کند، دوره تناوب اصلی یا دوره تناوب تابع f می گوییم و آن را با T نمایش می دهیم.

نکته: اگر a,b و c اعداد حقیقی باشند و a,b≠0 باشند در این صورت:

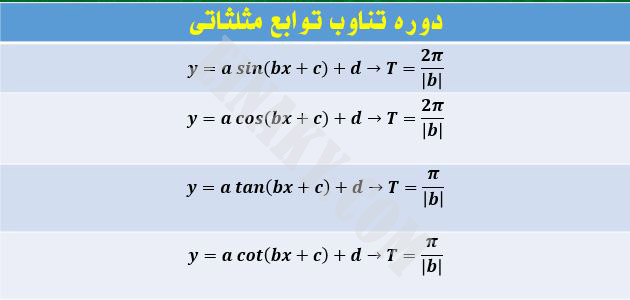
نکته: به طور کلی در توابع y=a cos(bx+d)+c , y=a sin(bx+c)+d

Max=|a|+c

Min=-|a|+c

C=(max+min)/2

نکته: اگر f تابعی متناوب و T دوره تناوب اصلی آن باشد، آنگاه برای هر عدد طبیعی N داریم:

(F(x±nT)=f(x

حل معادلات مثلثاتی

برای حل معادلات مثلثاتی، طرفین معادله را آنقدر ساده میکنیم تا به یکی از چهار حالت زیر برسیم، سپس با استفاده از دستور های زیر، جواب های کلی معادله را تعیین میکنیم.

حالات خاص معادلات مثلثاتی

در صورتی که به یکی از حالات زیر برسیم، به کمک دستورات زیر، جواب معادلات را تعیین می کنیم:

نکته: همواره برای تبدیل کردن  سینوس به کسینوس و بالعکس و نیز تانژانت به کتانژانت و بالعکس، از زاویه متمم یعنی π/2-α استفاده می کنیم.

نکته: اگر طرفین معادلات مثلثاتی هم جنس باشند، ولی یک طرف آن منفی باشد، در مورد سینوس، تانژانت و کتانژانت، علامت منفی را به داخل کمان می بریم.

ولی در مورد کسینوس علامت منفی را حذف کرده و زاویه α  را به π-α تبدیل می کنیم.

نکته: در معادلات کسری و رادیکالی، جواب هایی که در دامنه معادله نیستند را حذف می کنیم.

نکته: برای یافتن جواب های معادله در یک بازه، در معادله کلی به جای k، مقادیر مختلف صحیح را قرار داده و مقادیری از جواب که در بازه مربوطه قرار دارند را به دست می آوریم.

حتما بخوانید: تدریس فصل اول حسابان دوازدهم