

قضیه: فرض کنید تابع f در بازه [a,b] پیوسته و در بازه (a,b) مشتق پذیر باشد. در این صورت:
الف) اگر برای هر (f′ (x)>0,x∈(a,b باشد، آنگاه تابع f روی بازه [a,b] صعودی اکید است.
ب) اگر برای هر (f′ (x)<0,x∈(a,b باشد، آنگاه تابع f روی بازه [a,b] نزولی اکید است.
پ) اگر برای هر (f′ (x)=0,x∈(a,b باشد، آنگاه تابع f روی بازه [a,b] ثابت است.
نکته: شرط لازم برای استفاده از قضیه فوق این است که تابع f در بازه [a,b] پیوسته باشد.
اگر تابع f روی بازه I پیوسته باشد، برای تشخیص صعودی یا نزولی بودن تابع f ابتدا مشتق آن یعنی ‘f را محاسبه کرده و سپس آن را در یک جدول، تعیین علامت می کنیم.
به جدول تعیین علامت مشتق تابع f جدول تغییرات این تابع گفته می شود.
نکته: اگر تابع f در بازه I دارای مجانب قائم باشد، آن گاه تابع f روی بازه I غیر یکنوا است، حتی اگر ‘f در این بازه همواره مثبت یا همواره منفی باشد.
بدیهی است که استفاده از علامت مشتق در بخش هایی از بازه I که مجانب قائم در آن ها حضور ندارد و تابع F در آن قسمت ها پیوستگی داشته باشند، برای تشخیص یکنوایی معتبر است.
نکته: اگر تابع F روی بازه I ناپیوسته باشد، نمی توان از علامت تابع مشتق برای تعیین وضعیت یکنوایی تابع استفاده کرد.
بدیهی است که استفاده از علامت تابع مشتق روی بخش هایی از بازه که شامل نقاط ناپیوسته و تعریف نشده نیستند و تابع روی بخش ها پیوسته باشد، معتبر است.
در این حالت به کمک رسم نمودار یا محاسبه حدود چپ و راست و مقدار تابع (در صورت وجود) میتوان وضعیت یکنوایی تابع را در مجاورت نقطه ناپیوسته یا تعریف نشده تعیین نمود.
نکته: اگر چند تابع یکنوا و مشتق پذیر با یکدیگر ترکیب شده باشند، آن گاه برای تعیین وضعیت یکنوایی تابع مرکب حاصل کافی است علامت مشتق های آن ها را در هم ضرب کنیم، اگر علامت حاصل مثبت باشد تابع مرکب صعودی و چنان چه علامت حاصل منفی باشد، تابع مرکب نزولی است.
نقطه بحرانی: نقطه به طول C∈Df را نقطه بحرانی تابع f می گوییم هر گاه f’(c)=0 یا (f’(c موجود نباشد.
نکته: نقاط ابتدا و انتهای دامنه تابع نقاط بحرانی نیستند.
اگر نمودار تابع f را در اختیار داشته باشیم، آن گاه نقاط زیر روی نمودار تابع f، به شرط آن که نقطه درون دامنه این تابع باشند بحرانی هستند.
1- نقاط ناپیوسته
2- نقاط گوشه ای (زاویه دار)
3- نقاط با مماس قائم
4- نقاط با مماس افقی
اگر ضابطه تابع f را در اختیار داشته باشیم، برای یافتن نقاط بحرانی آن به صورت زیر عمل می کنیم:
1- در توابع تک ضابطه ای و بدون قدر مطلق و براکت از تابع مشتق گرفته و ریشه های صورت و مخرج را می یابیم، نقاط به دست آمده اگر به نقاط درونی دامنه تعلق داشته باشد، بحرانی اند.
2- در توابع چند ضابطه ای علاوه بر تعیین ریشه های صورت و مخرج تابع مشتق (در صورت وجود) نقاط مرزی را از لحاظ پیوستگی و مشتق پذیری بررسی می کنیم.
نکته: اگر تابع f تابعی مشتق پذیر باشد، آنگاه نقاط بحرانی تابع |(y=|f(x از حل معادلات مقابل به دست می آید:
اگر تابع g و f توابعی مشتق پذیر باشد، آنگاه نقاط بحرانی تابع |(y=g(x)|f(x از حل معادلات مقابل به دست می آید:
نکته: مجموعه نقاط بحرانی تابع [(y=[f(x با مجموعه نقاط درونی دامنه تابع f برابر است.
فرض کنید تابع f روی بازه I پیوسته باشد. اگر نمودار ‘f را در بازه I در اختیار داشته باشیم، نقاط به طول های زیر روی نمودار ‘f طول نقاط بحرانی تابع f هستند:
1- طول نقاط تلاقی نمودار ‘f با محور x ها
2- طول نقاط تعریف نشده و طول نقاطی که نمودار ‘f در آن نقطه پرش دارد.
3- طول نقاط مجانب قائم نمودار ‘f
ماکسیمم مطلق: فرض کنید C∈Df باشد، در این صورت (f(c مقدار ماکسیمم مطلق تابع f روی دامنه آن است، هر گاه برای هر x∈Df داشته باشیم:
(f(x)≤f(c
زمانی که می گوییم ماکسیمم مطلق تابع f در x=c اتفاق افتاده است، یعنی (f(c مقدار ماکسیمم مطلق و ((c,f(c) نقطه ماکسیمم مطلق تابع است.
نکته: به مقدار ماکسیمم مطلق تابع f به اختصار مقدار ماکسیمم یا ماکسیمم نیز گفته می شود.
مینیمم مطلق: فرض کنید C∈Df باشد، در این صورت (f(c مقدار مینیمم مطلق تابع f روی دامنه آن است، هر گاه برای هر x∈Df داشته باشیم:
(f(c)≤f(x
زمانی که می گوییم مینیمم مطلق تابع f در x=c اتفاق افتاده است، یعنی (f(c مقدار مینیمم مطلق و ((c,f(c) نقطه مینیمم مطلق تابع است.
نکته: به مقدار مینیمم مطلق تابع f به اختصار مقدار مینیمم یا مینیمم نیز گفته می شود.
(F(c را مقدار اکسترمم مطلق یا به اختصار مقدار اکسترمم یا اکسترمم تابع f گوییم هرگاه (f(c ماکسیمم یا مینیمم مطلق تابع f باشد.
نکته: با توجه به تعریف، مقدار ماکسیمم و مینیمم مطلق در یک تابع منحصر به فرد است اما طول نقاط ماکسیمم و مینیمم مطلق ممکن است منحصر به فرد نباشد.
نکته: لازم نیست تابع در همسایگی نقطه اکسترمم مطلق تعریف شده باشد، بنابر این اکسترمم مطلق تابع می تواند در نقاط ابتدایی یا انتهایی و نیز نقاط منفرد دامنه تابع رخ دهد.
اگر تابع f روی بازه بسته [a,b] پیوسته باشد، در این بازه دارای ماکسیمم و مینیمم مطلق است.
نکته: اگر حداقل یکی از شرایط قضیه فوق برقرار نباشد، یعنی تابعf پیوسته نباشد و یا بازه داده شده از دو طرف بسته نباشد آنگاه تابعf الزاماً ماکسیمم و مینیمم مطلق ندارد.
نکته: عکس قضیه وجود مقدار اکسترمم همیشه برقرار نیست.
یعنی اگر تابع f روی یک بازه دارای ماکسیمم و مینیمم مطلق باشد، نمیتوان نتیجه گرفت که F روی آن بازه پیوسته است.
نکته: اکسترمم های مطلق تابع f در صورت وجود در نقاط زیر اتفاق می افتد:
1- نقاط بحرانی f
2- نقاط ابتدایی و انتهایی بازه یا دامنه
فرض کنید تابع f روی بازه بسته [a,b] پیوسته باشد. در این صورت برای تعیین اکسترمم های مطلق و برد تابع به صورت زیر عمل می کنیم:
نقاط بحرانی تابع f را در بازه [a,b] تعیین می کنیم سپس مقادیر تابع f را در نقاط بحرانی و هم چنین (f(a),f(b را محاسبه می کنیم، از بین مقادیر به دست آمده بیشترین مقدار ماکسیمم مطلق و کمترین مقدار ، مینیمم مطلق است.
اگر ماکسیمم و مینیمم مطلق را به ترتیب با Mوm نشان دهیم برد تابع برابر [m.M] خواهد بود.
اگر تابع F روی بازه I پیوسته و بازه I حداقل از یک طرف باز باشد، آنگاه برای تعیین ماکسیمم مینیمم مطلق همانند قبل عمل می کنیم، با این تفاوت که اگر مقدار ماکسیمم یا مینیمم فقط به ازای طرف باز بازه رخ دهد آنگاه تابع F در بازه I ماکسیمم یا مینیمم مطلق نخواهد داشت.
در این حالت برد تابع از همان طرفی که ماکسیمم یا مینیمم مطلق موجود نیست باز خواهد بود.
نکته: اکسترمم های مطلق تابع پیوسته f را هنگامی که بازه ای برای آن داده نشده باشد روی دامنه اش تعیین می کنیم.
در حل مسائل بهینه سازی با استفاده از مشتق، فرایند زیر را انجام میدهیم:
1- در صورت لزوم شکلی برای مسئله رسم کرده، و متغیر ها را روی آن تعریف می کنیم.
2- کمیتی که قرار است ماکسیمم یا مینیمم شود به صورت معادله ای از متغیر ها می نویسیم. به این معادله معادله هدف می گوییم.
3– اگر معادله هدف به صورت دو یا چند متغیر باشد رابطه بین متغیر ها را مشخص می کنیم.
این رابطه یا در صورت مسئله داده می شود و یا باید آن را به کمک شکلی که با توجه به مفروضات مسئله رسم کرده ایم، به این معادله معادله کمکی می گوییم.
4- با تلفیق معادلات کمکی و هدف،معادله هدف را به صورت تابعی از یک متغیر به دست می نویسیم و دامنه این تابع را تعیین می کنیم.
5- با استفاده از مشتق گیری و یافتن نقاط بحرانی مقادیر ماکسیمم یا مینیمم مورد درخواست مسئله را تعیین می کنیم.
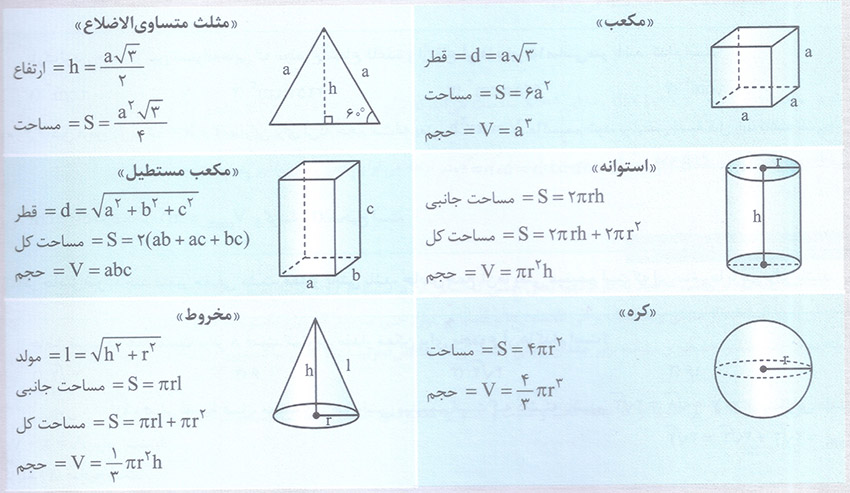
قضیه 1: اگر مجموع چند متغیر حقیقی و مثبت برابر مقدار ثابتی باشد، آنگاه حاصل ضرب آن ها وقتی ماکسیمم است که آن متغیر ها با هم مساوی باشند.
اگر ax+by=k که در آن a,b,k اعداد ثابت و مثبت و x,y متغیر های حقیقی و مثبت هستند آنگاه xy وقتی ماکسیمم است که داشته باشیم: ax=by=k/2
قضیه 2: اگر x1,x2,…,xn متغیرهای مثبت و دارای مجموعی ثابت باشند، آنگاه عبارت x1α,x2β,…x3γ وقتی ماکسیمم است که رابطه زیر برقرار باشد:
x1/α=x2/β=…xn/γ
نقطه به طول c∈Df را نقطه ماکسیمم نسبی تابع f می گوییم هر گاه اولاً تابع f در یک همسایگی c تعریف شده باشد و ثانیاً برای هر x در این همسایگی داشته باشیم: (f(x)≤f(c
مینیمم نسبی:
نقطه به طول c∈Df را نقطه مینیمم نسبی تابع f می گوییم هر گاه اولاً تابع f در یک همسایگی c تعریف شده باشد و ثانیاً برای هر x در این همسایگی داشته باشیم: (f(x)≥f(c
به نقاط ماکسیمم نسبی و مینیمم نسبی اکسترمم نسبی می گویند.
نکته: با توجه به تعریف نقطه اکسترمم نسبی، نقاط ابتدا و انتهای دامنه و نیز نقاط منفرد نمی توانند اکسترمم نسبی باشند.
نکته: هر نقطه در دامنه تابع ثابت f، به شرط آنکه تابع f در یک همسایگی آن نقطه تعریف شده باشد، هم ماکسیمم نسبی و هم مینیمم نسبی است.
1- مجموعه نقاط اکسترمم نسبی، زیر مجموعه نقاط بحرانی تابع است.
یعنی هر نقطه اکسترمم نسبی، بحرانی است و نه بر عکس.
2- هر نقطه اکسترمم مطلق که تابع در یک همسایگی آن تعریف شده باشد، اکسترمم نسبی است ولی نقاط اکسترمم نسبی همیشه اکسترمم مطلق نیستند.
اگر تابع f در نقاط بحرانی خود پیوسته باشد، ابتدا نقاط بحرانی را می یابیم و سپس به کمک تعیین علامت مشتق در جدول تغییرات (آزمون مشتق اول) نوع نقاط اکسترمم نسبی را تعیین می کنیم.
نکته: همواره ریشه های ساده یا مکرر از مرتبه فرد صورت و مخرج ‘f در صورتی که تابع f در همسایگی آن ها تعریف شده باشد نقاط اکسترمم نسبی تابع f هستند.
نکته: اگر f تابعی پیوسته و تعداد نقاط اکسترمم نسبی آن زوج باشد، نیمی از آن ها ماکسیمم و نیم دیگر مینیمم نسبی است.
1- اگر x=a طول نقطه اکسترمم نسبی تابع f و ‘f در x=a موجود باشد آنگاه f’(a)=0 است.
2- در حالت کلی از f’(a)=0 نمیتوان نتیجه گرفت که x=a طول اکسترمم نسبی تابع F است.
3- در حالت کلی اگر x=a طول اکسترمم نسبی f باشد، نمیتوان نتیجه گرفت که f’(a)=0
اگر (A(a,b نقطه اکسترمم نسبی تابع f و’f در نقطه A موجود باشد در این صورت:
1- f(a)=b
2- f’(a)=0
نکته: اگر (A(a,b نقطه اکسترمم نسبی تابع کسری fوf’ در نقطه A موجود باشد، آنگاه مختصات نقطه A هم در خود تابع و هم در هوپیتال تابع صدق می کند.
فرض کنید تابع f در بازه باز I شامل نقطه a پیوسته باشد، اگر نمودار ‘f را در اختیار داشته باشیم، در سه حالت زیر x=a طول اکسترمم نسبی تابع f است:
1- نمودار ‘f محور x ها را در x=a قطه کرده و از آن عبور می کند.
2- ‘f در x=a از محور x ها پرش داشته باشد.
3- x=a طول مجانب قائم با انفصال ساده نمودار ‘f باشد.(در همسایگی محذوفa , تابع f’ پیوسته است.)
نکته: اگر تابع f در نقاط بحرانی خود ناپیوسته باشد برای تعیین نوع نقاط اکسترمم نسبیf نمودار آن را رسم کنید.
فرض کنید تابع F در بازه I مشتق پذیر باشد در این صورت:
اگر در بازه I خطوط مماس بر منحنی تابع زیر منحنی قرار گیرند گوییم جهت تقعر تابع F رو به بالاست.
اگر در بازه I خطوط مماس بر منحنی تابع بالای منحنی قرار گیرند گوییم جهت تقعر تابع F رو به پایین است.
فرض کنید تابع F در بازه I مشتق پذیر باشد در این صورت:
اگر تابع ‘F روی بازه I صعودی اکید باشد، آنگاه جهت تقعر نمودار تابع F در این بازه رو به بالاست و بالعکس.
اگر تابع ‘F روی بازه I نزولی اکید باشد، آنگاه جهت تقعر نمودار تابع F در این بازه رو به پایین است و بالعکس.
اگر به ازای هر X∈I f′′ (x)=0 آزمون بی نتیجه است.
نکته: فرض کنیم تابع f در بازه i دوبار مشتق پذیر و x نقطه دلخواهی در i باشد، در این صورت گزاره های گروه آ با هم و گزاره های گروه ب نیز با هم معادل هستند.
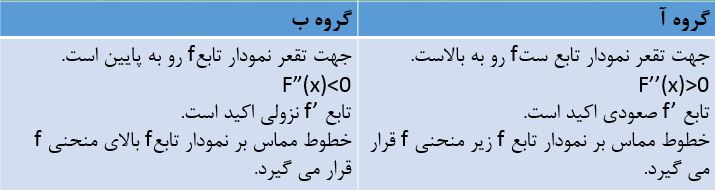
با توجه به قضیه تقعر برای تعیین جهت تقعر نمودار تابع f ابتدا “f را به دست آورده و سپس آن را تعیین علامت کنیم.
در هر بازه که علامت “f مثبت باشد، جهت تقعر تابع f رو به بالا و در هر بازه ای که “fمنفی باشد، جهت تقعر تابع f رو به پایین است.
نکته: فرض کنید تابع f روی بازه I مشتق پذیر باشد:
اگر تابع f در بازه i صعودی اکید یا نزولی اکید باشد آنگاه نمودار تابع ‘f در این بازه بالا یا پایین محور x ها قرار می گیرد و بالعکس.
فرض کنید تابع f روی بازه I دارای مشتق دوم و مشتق آن پیوسته باشد، در این صورت:
اگر جهت تقعر نمودار تابع f در بازه i رو به بالا یا رو به پایین باشد ، آنگاه ‘f در این بازه صعودی اکید یا نزولی اکید است و بالعکس
فرض کنیم تابع f در نقطه به طول x=c پیوسته باشد، در این صورت نقطه به طول x=c را نقطه عطف نمودار تابع F می گوییم، هر گاه دو شرط زیر به طور همزمان بر قرار باشد:
الف) نمودار تابع f در نقطه c دارای مماس واحد باشد، یعنی (f′+ (c)=f′– (c
ب) جهت تقعر تابع f در نقطه c عوض شود. به عبارت دیگر “f در c تغییر علامت دهد.
نکته: از شرط اول تعریف نقطه عطف تابع f نتیجه می شود که یا (f’(c موجود است و یا f در c مماس قائم دارد.
هم چنین از شرط دوم تعریف نقطه عطف نتیجه می شود که مماس بر منحنی در نقطه عطف از منحنی در همین نقطه عبور می کند.
زیرا جهت تقعر منحنی در یک طرف نقطه c رو به بالا و در طرف دیگر آن رو به پایین است و در نتیجه خط مماس بر منحنی در نقطه عطف در یک طرف نقطه c زیر منحنی و در طرف دیگر آن بالای منحنی قرار می گیرد.
نکته: در توابع تک ضابطه ای و بدون قدر مطلق و براکت، ریشه های ساده یا مکرر از مرتبه فرد صورت یا مخرج “f در صورتی که تابع در همسایگی این نقاط تعریف شده باشد، نقطه عطف تابع f هستند.
نکته: تابع درجه سوم f(x)=〖ax〗^3+〖bx〗^2+cx+d همواره دارای یک نقطه عطف به طول x=(-b)/3a است که این نقطه مرکز تقارن نمودار می باشد، یعنی تمام نقاط نمودار نسبت به نقطه عطف متقارن هستند.
در توابع چند ضابطه ای علاوه بر جستجوی نقطه عطف در نقاط درونی هر یک از ضابطه ها، نقاط مرزی را نیز باید از نظر عطف بودن بررسی کنیم.
در واقع اگر c∈Df طول نقطه مرزی تابع چند ضابطه ای f باشد، انگاه c طول نقطه عطف تابع f است اگر و تنها اگر دو شرط زیر برقرار باشد:
(f”+ (c).f”– (c)<0 f′+ (c)=f′– (c
فرض کنید تابع f روی بازه باز I شامل نقطه به طول a پیوسته باشد.
اگر نمودار f’ را در اختیار داشته باشیم در دو حالت زیر x=a طول نقطه عطف تابع f می باشد:
الف) x=a طول نقطه اکسترمم نسبی تابع ‘f باشد به شرط آن که در هیچ همسایگی چپ یا راست a ثابت نباشد.
ب) خط x=a مجانب قائم با انفصال مضاعف تابع ‘f باشد (f در همسایگی محذوف a دارای مشتق پیوسته است.)
1- دامنه تابع را تعیین می کنیم.
2- نقاط تلاقی با محور های مختصات را در صورت امکان به دست می آوریم.
3- از تابع مشتق می گیریم و به کمک مشتق، جهت تغییرات تابع یعنی صعودی یا نزولی بودن تابع و نیز نقاط بحرانی و اکسترمم های نسبی تابع را تعیین می کنیم.
4- مشتق دوم تابع را محاسبه کرده و به کمک تعیین علامت آن، جهت تقعر تابع و نقاط عطف تابع را مشخص می کنیم.
5- مجانب های تابع را در صورت وجود می یابیم.
6- رفتار تابع را به ازای مقادیر بسیار بزرگ و بسیار کوچک x مشخص میکنیم.
7- جدولی به نام جدول رفتار تابع تنظیم می کنیم که کلیه اعمال انجام شده در قسمت های قبل در آن درج شده باشد.
در این جدول مقدار یا حد تابع در نقاط اکسترمم نسبی، عطف و نقاط انتهایی دامنه و نیز حد تابع را در اطراف نقاط تعریف نشده تعیین می کنیم.
8- به کمک جدول رفتار تابع نمودار تابع را رسم میکنیم.
1- دامنه تابع برابر R و تابع روی R پیوسته و مشتق پذیر است.
2- مشتق این تابع برابر y′=3ax2+2bx+c که تابعی درجه دوم است و بر حسب این که مشتق تابع دارای دو جواب متمایز یا دارای جواب مضاعف یا فاقد جواب است.
نمودار تابع درجه سوم به ترتیب دارای دو اکسترمم نسبی بوده یا فاقد اکسترمم نسبی و در نقطه عط آن خط موازی محور x ها است و یا این که فاقد اکسترمم نسبی بوده و مماس افقی ندارد.
بنابر این اگر a>0 باشد،آنگاه نمودار این تابع از ربع سوم شروع شده و به ربع اول ختم می شود و چنان چه a<0 باشد، نمودار این تابع از ربع دوم شروع شده و به ربع چهارم ختم می شود.
3- تابع درجه سوم همواره دارای یک نقطه عطف می باشد که مرکز تقارن نمودار تابع نیز هست و طول آن از رابطه x=(-b)/3a به دست می اید.
4- در حالتی که نمودار تابع درجه سوم دارای یک ماکسیمم نسبی و یک مینیمم نسبی است.
نقاط ماکسیمم مینیمم نسبی و عطف تابع هر سه روی یک خط راست واقع اند، و نقطه عطف وسط پاره خط واصل بین نقاط ماکسیمم و مینیمم نسبی است:
xعطف=y (xmax+xmin)/2 عطف=ymax+ymin)/2)
5- هر خطی که از نقطه عطف تابع درجه سوم بگذرد و نمودار تابع را علاوه بر نقطه عطف در دو نقطه دیگر نیز قطع کند، آنگاه به دلیل مرکز تقارن بودن نقطه عطف، پاره خط های جدا شده روی خط با هم برابر هستند.
نکته: اگر خط افقی y=k منحنی تابع درجه سوم را قطع کند و بر روی آن دو پاره خط مساوی ایجاد کند آنگاه y=k عرض نقطه عطف منحنی است.
1- هر تابع کسری با ضابطه (f(x)=(ax+b)/(cx+dبا شرط c≠0 و ad-bc≠0 را یک تابع هموگرافیک می گویند.
2- اگر c=0 آنگاه ضابطه تبع به صورت f(x)=a/d x+b/d در می آید که یک خط راست بوده و خواص تابع هموگرافیکی را ندارد.
3- اگرad-bc=0 آنگاه این تابع به یک تابع یک به یک و ثابت تبدیل می شود که باز هم خواص تابع هموگرافیکی را ندارد.
1- دامنه تابع هموگرافیک (f(x)=(ax+b)/(cx+d برابر {R-{-d/c و برد آن برابر {R-{a/c بوده و این تابع روی دامنه خود پیوسته و مشتق پذیر است.
2- نمودار تابع همواره دارای یک مجانب قائم به معادله x=(-d)/c (ریشه مخرج) و یک مجانب افقی به معادله y=a/c (مقدار حد در بی نهایت) است.
3- نمودار تابع دارای دو محور تقارن عمود بر هم با شیب های 1 و -1 می باشد که از مرکز تقارن تابع می گذرند.
پس معادلات محورهای تقارن این تابع به صورت زیر است:
y=x+(a+d)/c , y=-x+(a-d)/c
5- مشتق تابع به صورت y′=(ad-bc)/(cx+d)2
می باشد و چون ad-bc≠0 لذا مشتق تابع هر گز صفر نمی شود و در نتیجه تابع هرگز صفر نمی شود و در نتیجه تابع هموگرافیک نقطه بحرانی ندارد.
نکته: شرط آنکه تابع هموگرافیک روی بازه I صعودی اکد یا نزولی اکید باشد آن است که:
الف) ad -bc>0یا ad-bc<0
ب) مجانب قائم تابع به بازه I تعلق نداشته باشد یعنی d/c∉I-
در اغلب تست های مربوط به رسم نمودار ضابطه یک تابع همراه با یک یا چند پارامتر و نیز نمودار آن داده می شود و ما باید پارامتر های موجود را به دست آوریم.
در این گونه تست ها باید با دقت زیاد اطلاعاتی را که در نمودار تابع یا ضابطه آن وجود دارد و منجر به حل مسئله می شود، استخراج نمود.
در استخراج اطلاعات به کار بستن موارد زیر می تواند کار ساز باشد:
1- مقایسه ی دامنه تابع و دامنه ی نمودار
2- توجه به محل و تعداد نقاط تلاقی نمودار با محور های مختصات
نکته: اگر نمودار تابع مشتق پذیر f بر محور x ها مماس شده باشد، آنگاه معادله f(x)=0 جواب مضاعف دارد.
بدیهی است که اگر تابع f کسری باشد، آنگاه در این حالت، صورت کسر ریشه ی مضاعف دارد.
نکته: در معادله درجه دوم ax^2+bx+c=0 اگر Δ=0 باشد، معادله ریشه مضاعف دارد و ریشه مضاعف این معادله از رابطه x=(-b)/2a به دست می آید.
3- بررسی وضعیت تابع در اطراف مجانب ها و مد نظر قرار دادن برخورد مجانب با نمودار و محور های مختصات
نقطه توخالی روی نمودار، در صورتی که تابع در این نقطه دارای حد باشد، هم ریشه صورت کسر است و هم ریشه مخرج کسر
5- بررسی وضعیت نقاط اکسترمم نسبی تابع
اگر (A(a,b نقطه اکسترمم نسبی نمودار تابع f بوده و f در این نقطه مشتق پذیر باشد ،آنگاه:
مختصات نقطه A در معادله تابع صدق می کند یعنی f(a)=b
مشتق تابع به ازای طول نقطه اکسترمم نسبی صفر است. یعنی f’(a)=0
نکته: اگر فقط طول نقطه اکسترمم نسبی مشخص باشد، و تابع در این نقطه مشتق پذیر باشد، آنگاه مشتق تابع به ازای طول نقطه اکسترمم نسبی صفر است.
نکته: اگر فقط عرض نقطه اکسترمم نسبی مشخص و برابر y=b بوده و تابع در این نقطه مشتق پذیر باشد، آنگاه معادله تلاقی تابع با خط y=b جواب مضاعف خواهد داشت.
6- توجه به نقطه عطف تابع
اگر (A(a,b نقطه عطف تابع f باشد و تابعf در نقطه A دارای مشتق دوم باشد آنگاه:
مختصات نقطه A در معادله صدق می کند. یعنی F(a)=0
مشتق دوم به ازای طول نقطه عطف صفر است. یعنی f’’(a)=0
7- مقایسه دوره تناوب تابع و دوره تناوب نمودار آن در توابع متناوب
در توابع متناوب مانند اغلب توابع مثلثاتی میتوان به کمک دوره تناوب تابع پارامتر های موجود در ضابطه را به دست آورد.
همون آموزشی که دنبالش بودی: تدریس فصل 4 حسابان دوازدهم