

شیب خط مماس بر منحنی تابع f در نقطه ((A(a,f(a یا همان شیب منحنی در نقطه A از رابطه زیر به دست می آید:
(m=lim(x→a)f(x)-f(a)/(x-a
به خطی که از نقطه ((A(a,f(a بگذرد و شیب آن برابر حد فوق باشد، خط مماس بر منحنی تابع f در نقطه ((A(a,f(a میگوییم.
نکته:اگر تابع f در نقطه x=a پیوسته باشد و ±∞=(m=lim(x→∞)f(x)-f(a)/(x-a آنگاه به خط x=a مماس قائم بر نمودار تابع f در نقطه ((A(a,f(a می گوییم.
نکته: اگر x=a مماس قائم بر نمودار f نباشد و نیز (lim(x→a)f(x)-f(a)/(x-a موجود نباشد، آنگاه مماس بر منحنی تابع f در نقطه ((A(a,f(a تعریف نمی شود.
فرض کنید تابع f در همسایگی نقطه x=a تعریف شده باشد، اگر
(lim(x→a)f(x)-f(a)/(x-a موجود و متناهی باشد، می گوییم تابع f در نقطه x=a مشتق پذیر و یا دارای مشتق است و مقدار این حد را با (f′(a نمایش می دهیم. بنابر این داریم:
(f′ (a)=lim(x→a)f(x)-f(a)/(x-a
نکته: با استفاده از تغییر متغیر x=a+h تعریف مشتق به صورت مقابل در می آید:
f′ (a)=lim(h→0)f(a+h)-f(a)/h
بنابر این مشتق تابع f در نقطه x=a به دو صورت مقابل است:
f′ (a)=lim(x→a)f(x)-f(a)/(x-a)=lim(h→0)f(a+h)-f(a)/h
به شرط آنگه حدود فوق موجود و متناهی باشد.
مشتق های راست و چپ تابع f را با (f′+ (a و (f′– (a نمایش داده و به صورت زیر تعریف می کنیم:
f′+ (a)=lim(x→a+ )f(x)-f(a)/(x-a)=lim(h→0+ )f(a+h)-f(a)/h
f′– (a)=lim(x→a- )(f(x)-f(a))/(x-a)=lim(h→0– )(f(a+h)-f(a))/h
F در x=a مشتق پذیر← F در x=a پیوسته
F در x=a ناپیوسته ← F در x=a مشتق ناپذیر
F در x=a پیوسته⇍ F در x=a مشتق پذیر
نکته: مطالب فوق برای مشتق های یک طرفه نیز درست است.
تابع f در x=a مشتق ناپذیر است، هرگاه یکی از شرایط زیر برقرار باشد:
1- f در x=a ناپیوسته باشد.
2- f در x=a پیوسته باشد و مشتق های چپ و راست در x=a:
الف) هر دو موجود ولی نابرابر باشند.
ب) یکی متناهی و دیگری نامتنهاهی باشد.
نکته: نقطه مشتق پذیر x=a را در این حالت نقطه گوشه ای یا نقطه زاویه دار می نامند.
3- F در x=a پیوسته باشد و مشتق های چپ و راست در x=a:
الف) هر دو نامتناهی ولی برابر باشند.
ب) هر دو نامتناهی ولی نابرابر باشند.
نکته: نقطه مشتق پذیر در x=a را در قسمت الف نقطه عطف قائم و در قسمت ب نقطه بازگشتی می نامند.
تابع f در x=a دارای مماس قائم است هر گاه:
1- f در x=a پیوسته باشد.
2- ∞-=(f’(a یا ∞+=(f’(a
x=a طول نقطه گوشه ای تابع f است هر گاه:
1- F در x=a پیوسته باشد.
2- (f′– (a و (f′+ (a هر دو عدد و نابرابر و یا حداکثر یکی از آن ها نامتناهی باشد.
1-توابع چند جمله ای: روی R مشتق پذیرند و نقطه مشتق ناپذیر ندارند.
2- توابع ((y=sin(p(x و (y=cos(p(x)) p(x چند جمله ای است: روی R مشتق پذیرند و نقطه مشتق ناپذیر ندارند.
3- توابع کسری گویا: فقط در ریشه های مخرج کسر مشتق ناپذیرند.
4- توابع قدر مطلقی به فرم y=g(x)|f(x)| f , g مشتق پذیر: در ریشه های ساده درون قدر مطلق مشتق ناپذیرند مگر آنکه بیرون قدر مطلق در آن ریشه ساده، عامل صفر کننده داشته باشد.
5- توابع رادیکالی:
الف: توابع رادیکالی با فرجه فرد به شکل (f(x)=2n+1√(x-a)m g(x
که در آن g در x=a مشتق پذیر و g(a)≠0 و m وn اعداد طبیعی هستند، در x=a وقتی مشتق پذیر است که m≥2n+1 و در حالتی که m<2n+1 باشد،f در x=a مشتق ناپذیر است.
ب- توابع رادیکالی با فرجه زوج به شکل (f(x)=n√(x-a)m g(x
که در آن g در x=a مشتق پذیر و g(a)≠0 و m وn اعداد طبیعی هستند، در x=a وقتی پشتق پذیر است که m زوج بوده و m>2n و f در همسایگی x=a تعریف شده باشد. در غیر این صورت f در x=a مشتق ناپذیر است.
6- توابع چند ضابطه ای: نقاط مشتق ناپذیر این توابع به یکی از دو صورت زیر است:
الف) نقاطی که هر ضابطه با توجه به دامنه اش در آن نقاط مشتق ناپذیر است.
ب) احتمالاً نقاط مرزی تابع که باید مشتق پذیری در این نقاط بررسی شود.
7- توابع شامل براکت: فرض کنید توابع f و g در x=a مشتق پذیر بوده و
[(h(x)=f(x)[g(x در این صورت:
الف) اگر g(a)∉z آنگاه تابع h در x=a پیوسته و مشتق پذیر است.
ب) اگر g(a)∈z و x=a طول نقطه مینیمم نسبی تابع g باشد آنگاه تابع h ر x=a مشتق پذیر است.
پ) اگر g(a)∈z و x=a ریشه مضاعف یا مکرر تابع f باشد آنگاه تابع h در x=aمشتق پذیر است.
ت)اگر g(a)∈z و x=a ریشه ساده تابع f بوده و تابع [(g(x] در x=a حد داشته باشد باز هم تابع h در x=a مشتق پذیر است.
ث) در غیر صورت های فوق تابع h در x=a مشتق ناپذیر می باشد.
8- مشتق پذیری روی یک بازه
الف) تابع f روی بازه (a,b) مشتق پذیر است هرگاه در هر نقطه از این بازه مشتق پذیر باشد.
ب) تابع f روی بازه [a,b] مشتق پذیر است هرگاه در بازه (a,b) مشتق پذیر باشد و در x=a مشتق راست و درx=b مشتق چپ داشته باشد.
پ) تابع f روی بازه [a,b) مشتق پذیر است هرگاه در بازه (a,b) مشتق پذیر باشد و در x=a مشتق راست داشته باشد.
ت) تابع f روی بازه (a,b] مشتق پذیر است هرگاه در بازه (a,b) مشتق پذیر باشد و در x=b مشتق چپ داشته باشد.
تابع مشتق تابع F به ازای هر x∈Df عبارت است از :
f′(x)=lim(h→0)f(x+h)-f(x)/h
به شرط آنکه حد فوق موجود باشد.
نکته: تابع مشتق تابع (y=f(x را با نمادهای f′ (x),y′,dy/dx,df/dx نیز نمایش می دهند.
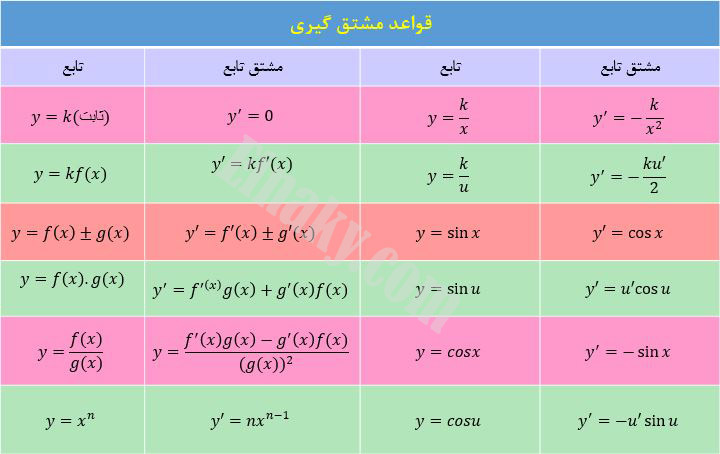
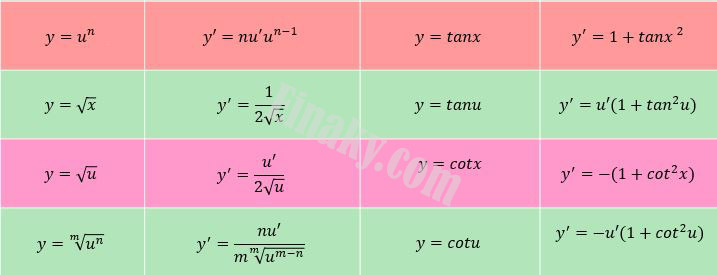
1- اگر ضابطه ساده شدنی بود، بهتر است قبل از مشتق گیری آن را ساده کنیم.
2- اگر قانون تابع f به صورت حاصل ضرب دو یا چند عمل باشد به طوری که یکی از آنها به ازای x=a صفر شود، برای محاسبه (f’(a کافی است از عامل صفر شونده مشتق گرفته و سپس x=a را در مشتق و عوامل غیر صفر جایگذاری کنیم.
نکته: اگر توان عامل صفر شونده بیشتر از 1 باشد، مشتق در آن نقطه برابر صفر می شود.
3- برای محاسبه مشتق توابع قدر مطلق در x=a به طوری که x=a ریشه درون قدر مطلق نباشد، ابتدا عبارت درون قدر مطلق را در همسایگی x=a تعیین علامت کرده و قدر مطلق را برداریم و سپس از آن مشتق می گیریم.
4- برای محاسبه مشتق توابع شامل براکت در x=a ابتدا حاصل براکت را در همسایگی x=a به دست آورده و براکت را بر میداریم و سپس از آن مشتق می گیریم.
روش اول: تابع مشتق تابع f را می یابیم، و سپس دامنه تابع ‘f را تعیین می کنیم.
روش دوم: نقاط مشتق ناپذیر تابع f را تعیین می کنیم و آن ها را از دامنه تابع f کم می کنیم.
1- اگر ضابطه تابع f معلوم باشد، ابتدا ضابطه ‘f را محاسبه کرده و سپس نمودار آن را رسم می کنیم.
2- اگر تنها نمودار تابع f را در اختیار داشته باشیم، برای رسم نمودار تابع ‘f از نکته زیر استفاده می کنیم:
نکته: فرض کنید تابع f روی بازه i مشتق پذیر باشد، در این صورت:
الف) اگر نمودار f روی بازه I اکیداً صعودی باشد، آنگاه نمودار تابع ‘F در بازه I همواره بالای محور x ها قرار می گیرد.
ب) اگر نمودار f روی بازه I اکیداً نزولی باشد، آنگاه نمودار تابع ‘F در بازه I همواره زیر محور x ها قرار می گیرد.
پ) اگر نمودار f روی بازه I ثابت باشد، آنگاه نمودار تابع ‘F’ در بازه I همواره بر محور x ها منطبق خواهد بود.
ت) در هرنقطه از بازه I که مماس بر منحنی F افقی باشد، نمودار تابع ‘F در آن نقطه محور x ها را قطع می کند.
(h(x)=(fog)(x)⟹h′ (x)=g′ (x)f′g(x
نکته: اگر u تابعی از x باشد، آنگاه:
(y=f(u)⟹y′=u′ f′(u
اگر y تابعی از u و u تابعی از x باشد آنگاه:
dy/dx=dy/du×du/dx
اگر (y=f(x یک تابع باشد، آنگاه به (y’’=f’’(x مشتق تابع f می گوییم.
شرایط وجود مشتق مرتبه دوم
توابع f و’f در x=a پیوسته باشند.
(f+′′ (a)=f-′′ (a و متناهی باشند.
خط مماس:خطی که شیب آن (f’(a بوده و از نقطه ((A(a,f(a می گذرد.
خط قائم: خطی که در نقطه ((A(a,f(a بر خط مماس عمود است و لذا شیب آن
(-1)/(f′(a می باشد.
معادلات خطوط مماس و قائم بر منحنی f در نقطه ((A(a,f(a واقع بر منحنی به صورت زیر است:
خط مماس: (y-f(a)=f′(a)(x-a
خط قائم: (y-f(a)=-1/f′ (a) (x-a
نکته: معادله خطی که از نقطه ((A(a,f(a بگذرد و شیب آن ∞ باشد به صورت x=a است.
شرط مماس بودن دو منحنی بر هم
شرط اینکه دو منحنی (y=f(xو (y=g(x در x=a بر هم مماس باشند آن است که :
(f(a)=g(a),f′ (a)=g′(a
اگر معادله تلاقی دو منحنی یعنی معادله (f(x)=g(x یک معادله درجه دوم باشد میتوان به جای دو شرط فوق شرط 0=∆ را اعمال کرد.
آهنگ متوسط تغییر تابع f نسبت به x در بازه ای مانند [a,a+h] عبارت است از :
Δf/Δx=f(a+h)-f(a)/h
آهنگ متوسط تغییر تابع f نسبت به x وقتی متغییر x از x1 به x2 تغییر می کند برابر است با :
Δf/Δx=f(x2 )-f(x1)/x2-x1
آهنگ لحظه ای یا آنی تغییر و یا به اختصار آهنگ تغییرات تابع f نسبت به x در x=a عبارت است از :
(lim(h→0)f(a+h)-f(a)/h=f′(a
نکته: وقتی گفته می شود آهنگ تغییر مقصود آهنگ لحظه ای یا آنی تغییرات است و آهنگ متوسط تغییر به صراحت قید می شود.
آهنگ متوسط تغییر با شیب خط قاطع و آهنگ لحظه ای تغییر با مفهوم مشتق در یک نقطه متناظر هستند.
نکته: آهنگ متوسط تغییرات تابع درجه دوم f(x)=ax2+bx+c نسبت به x روی بازه [α,β] با آهنگ آنی تغییرات تابع f در وسط این بازه یعنی x0=(α+β)/2 برابر است.
نکته: آهنگ لحظه ای تغییر تابع f نسبت به تابع g برابر است با :
(f′g=f′(x)/g′(x
سرعت و شتاب لحظه ای
اگر معادله مکان یک متحرک بر حسب زمان t برابر (x(t باشد، در این صورت:
الف) سرعت متوسط متحرک در فاصله زمانی [t1,t2] برابر است با:
v ̅=Δx/Δt=x(t2 )-x(t1)/t2-t1
ب) سرعت لحظه ای متحرک در لحظه t=t0 برابر است با:
(v ̅(t0 )=x′(t0
پ) شتاب متوسط در فاصله زمانی [t1,t2] برابر است با:
a ̅=Δv/Δt=v(t2 )-v(t1)/t2-t1
ت) شتاب لحظه ای متحرک در لحظهt=t0 برابر است با:
(a(t)=(v′) ̅(t0 )=x′′(t0
اگر (x(t معادله حرکت یک متحرک روی محور x ها باشد، در این صورت:
1- اگر (x(0 مکان اولیه متحرک و (x’(0 سرعت اولیه متحرک است.
2- در هر بازه زمانی که x’(t)>0 باشد، متحرک در جهت مثبت محور و در هر بازه زمانی که x’(t)<0 باشد متحرک در جهت منفی محور در حرکت است.
3- در لحظاتی که x(t)=0 است، متحرک از مبدا عبور می کند.
نکته: اگر تابع f روی بازه I مشتق پذیر و اکیداً صعودی یا اکیداً نزولی باشد، آنگاه آهنگ تغییر متوسط f در این بازه همواره مثبت یا منفی و آهنگ تغییر لحظه ای f در این بازه نامنفی یا نامثبت است.
فرض کنید تابع f روی بازه [a,b] مشتق پذیر باشد، در این صورت:
الف) اگر گودی یا تقعر منحنی f در این بازه رو به بالا باشد، آنگاه آهنگ متوسط و لحظه ای تغییر f در این بازه اکیداً صعودی است.
ب) اگر گودی یا تقعر منحنی f در این بازه رو به پایین باشد، آنگاه آهنگ متوسط و لحظه ای تغییر f در این بازه اکیداً نزولی است.
پ) اگر تابع f در این بازه تابعی خطی باشد، آنگاه آهنگ متوسط و لحظه ای تغییر f در این بازه ثابت است.
فرض کنید تابع f روی بازه [a,a+h] مشتق پذیر باشد، در این صورت با تغییر h:
الف) اگر گودی یا تقعر منحنی f در این بازه رو به بالا باشد، آنگاه آهنگ متوسط تغییر f در بازه [a,a+h] از آهنگ لحظه ای تغییر f در a+h کوچکتر است.
ب) اگر گودی یا تقعر منحنی f در این بازه رو به پایین باشد، آنگاه آهنگ متوسط تغییر f در بازه [a,a+h] از آهنگ لحظه ای تغییر f در a+h بزرگتر است.
پ) اگر f تابعی خطی در این بازه باشد،آنگاه آهنگ متوسط تغییر f در بازه [a,a+h] با آهنگ لحظه ای تغییر f در a+h برابر است.
یک دیدگاه دربارهٔ «تدریس فصل چهارم حسابان دوازدهم (مشتق)»