
چند ضلعی
هر خط شکسته بسته، یک چند ضلعی است، به شرط آنکه ضلع ها یکدیگر را قطع نکنند.
سوال: به خط شکسته بسته که اضلاع همدیگر را قطع نکنند…. می گویند؟ چند ضلعی
- هر چند ضلعی به تعداد ضلع هایش زاویه دارد.

چند ضلعی منتظم: اگر در یک چند ضلعی تمام ضلع ها با هم و تمام زاویه ها با هم برابر باشند به آن چند ضلعی منتظم می گویند.
چند ضلعی محدب(کوژ)
اگر تمام زاویه های یک چند ضلعی از ۱۸۰ کوچکتر باشد،به آن چند ضلعی محدب می گویند.
چند ضلعی مقعر(کاو)
اگر یک چند ضلعی دارای حداقل یک زاویه بزرگتر از ۱۸۰ باشد، به آن چند ضلعی مقعر می گویند.

سوال: سه ضلعی منتظم چه نام دارد؟ مثلث متساوی الاضلاع
مرکز تقارن چند ضلعی
اگر نقطه ای مانند o در داخل یک چند ضلعی وجود داشته باشد به طوریکه قرینه هر نقطه از آن شکل، نسبت به نقطه o روی شکل واقع شود، می گوییم آن چند ضلعی دارای مرکز تقارن است.
- هر شکلی که دارای دو خط تقارن عمود بر هم است، نقطه برخورد دو خط تقارن عمود بر هم آن مرکز تقارن آن شکل است.
- عکس این مطلب درست نیست. یعنی اگر شکل دارای مرکز تقارن باشد، نمیتوان نتیجه گرفت که به طور حتم شکل دارای دو خط تقارن عمود بر هم است.
- هر n ضلعی منتظم به تعداد ضلع هایش زاویه و خط تقارن دارد.یعنی هر n ضلعی منتظم دارای n زاویه مساوی، n ضلع مساوی و n خط تقارن است.
سوال: چند ضلعی منتظم ….. خط تقارن دارد؟ چند ضلعی منتظم به تعداد اضلاعش خط تقارن دارد.
- در n ضلعی های منتظم که تعداد ضلع های آنها زوج است، محل تقاطع یا نقطه تقاطع خط های تقارن آنها، مرکز تقارن شکل است.
- n ضلعی های منتظم که تعداد اضلاع آنها فرد است، مرکز تقارن ندارند، یعنی نقطه ی تقاطع خط های آنها مرکز تقارن نیست.
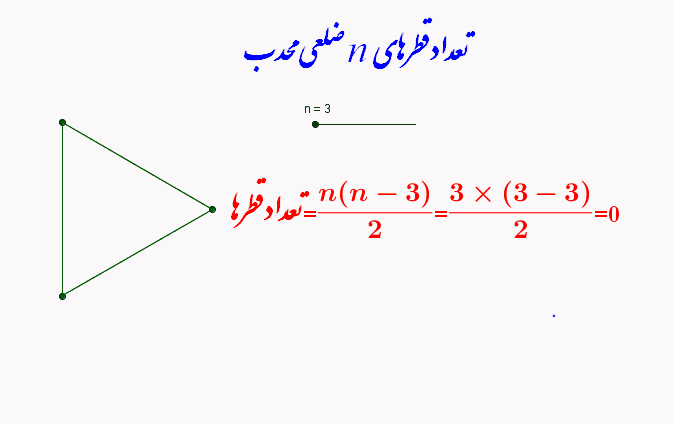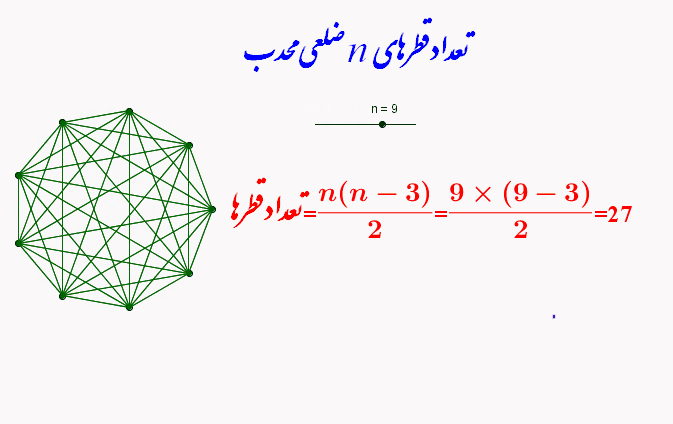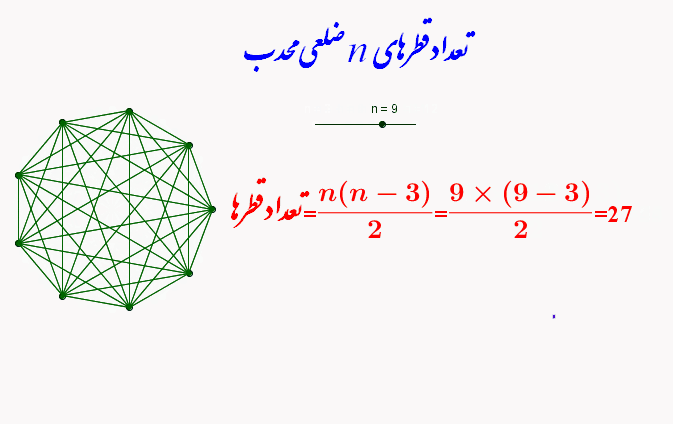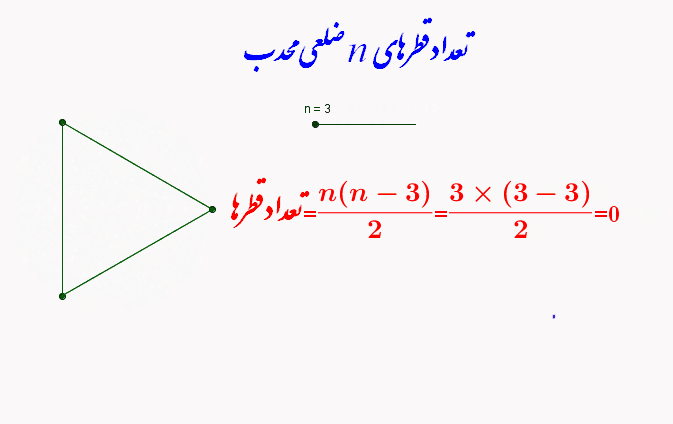
تعداد قطرهای n ضلعی محدب
توازی و تعامد
اگر خط d بر خط a عمود باشد به صورت ریاضی می نویسیم:
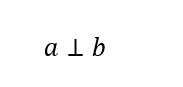
اگر دو خط a و b موازی باشند، به صورت ریاضی می نویسیم:
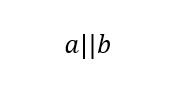
- نکته: اگر خطی بر دو خط موازی، عمود شود با آن دو خط ۸ زاویه مساوی، ۹۰ درجه به وجود می آورد.
- نکته: اگر خط موربی، دو خط موازی را قطع کند با آن هشت زاویه به وجود می آورد که چهار تا از زاویه ها تند و چهار تای دیگر باز هستند.
- نکته: زاویه های تند با هم و زاویه های باز با هم برابرند.
اصل توازی
- اصل اول: دو خط عمود بر یک خط با هم موازیند.
- اصل دوم: اگر خطی بر یکی از دو خط موازی عمود شود بر دیگری نیز عمود می شود.
- اصل سوم: دو خط موازی با یک خط خودشان با هم موازی هستند.
- نکته: فاصله دو خط موازی در تمامی نقاط همیشه یکسان است.
- نکته: از یک نقطه خارج یک خط فقط یک خط موازی با آن میتوان رسم کرد.
- نکته: از یک نقطه خارج یک خط فقط یک خط عمود بر آن میتوان رسم کرد.
رسم پاره خط موازی با یک پاره خط در یک صفحه شطرنجی
برای این کار فقط کافی است که دو نقطه aوb که دو سر یک پاره خط هستند را با یک بردار دلخواه انتقال دهیم.
- در مثلث متساوی الساقین ارتفاع وارد بر قاعده مثلث، عمود منصف قاعده، نیمساز زاویه راس و میانه وارد بر قاعده ی مثلث و خط تقارن نیز هست.
- در مثلث متساوی الاضلاع هر یک از ارتفاع های آن نیمساز میانه عمود منصف و خط تقارن مثلث نیز هست.

متوازی اضلاع
هر چهار ضلعی که ضلع های مقابل آن دو به دو موازی باشند، متوازی اضلاع است.
- در متوازی اضلاع ضلع های رو به رو با هم مساویند.
- در متوازی اضلاع زاویه های رو به رو با هم مساویند.
- در متوازی اضلاع قطرها همدیگر را نصف می کنند.
- در متوازی اضلاع زاویه های مجاور مکملند.
- در متوازی اضلاع قطرها با یکدیگر برابر نیستند.
- هر چهار ضلعی که دارای چهار زاویه قائمه باشد متوازی اضلاع است.
مستطیل، مربع و لوزی چون اضلاع مقابلشان دو به دو موازیند بنابر این هر کدام از این شکل ها متوازی اضلاع هستند و خواص متوازی اضلاع را دارند.

مستطیل: متوازی اضلاعی است که چهار زاویه قائمه دارد.
مربع: متوازی اضلاعی است که چهار ضلع مساوی و چهار زاویه قائمه دارد.
لوزی: متوازی اضلاعی است که چهار ضلع برابر دارد.
ذوزنقه: یک چهار ضلعی است که فقط دو ضلع موازی دارد و به همین دلیل متوازی اضلاع نیست.
چون مستطیل تمام خاصیت های متوازی اضلاع را دارد بنابر این مستطیل یک نوع متوازی اضلاع است.
اما متوازی اضلاع یک نوع مستطیل نیست چون تمام ویژگی های مستطیل را ندارد برای مثال چهار زاویه برابر ندارد.
-
در مستطیل قطر ها با هم برابرند.
مربع نوعی متوازی اضلاع است، چون تمام ویژگی های متوازی اضلاع را دارد .
اما متوازی اضلاع نوعی مربع نیست چون تمام ویژگی های مربع را ندارد برای مثال متوازی اضلاع چهار ضلع برابر ندارد.
لوزی نوعی متوازی اضلاع است چون تمام ویژگی های متوازی اضلاع را دارد .
اما متوازی اضلاع نوعی لوزی نیست چون تمام ویژگی های لوزی را ندارد برای مثال متوازی اضلاع دارای چهار ضلع برابر نیست.

- نکته: در لوزی قطرها بر هم عمودند و قطر ها نیم ساز زاویه های مقابلند.
- نکته: مربع نوعی لوزی است اما لوزی نوعی مربع نیست زیرا لوزی دارای چهار زاویه مساوی نیست.
- نکته: مربع نوعی مستطیل است، اما مستطیل مربع نیست.
- نکته: اگر وسط ضلع های کنار هم متوازی الاضلاع را به هم وصل کنیم از برخورد آنها یک متوازی الاضلاع حاصل می شود.

- نکته: اگر وسط ضلع های مجاور یک مستطیل را دو به دو به هم وصل کنیم از برخورد آنها یک لوزی حاصل می شود.
- نکته: اگر وسط ضلع های مجاور یک لوزی را دو به دو به هم وصل کنیم از برخورد آنها یک مستطیل به وجود می آید.
- نکته: اگر وسط ضلع های مجاور یک مربع را دو به دو به هم وصل کنیم از برخورد آنها یک مربع حاصل می شود.
- نکته: هر چهار ضلعی که فقط دو ضلع موازی داشته باشد، ذوزنقه نامیده می شود.
- نکته: به دو ضلع موازی ذوزنقه قاعده و به دو ضلع غیر موازی ساق می گویند.
- نکته: در هر ذوزنقه ای زاویه های مجاور به هر ساق مکمل اند(مجموع آنها ۱۸۰ است)
- نکته: فقط در ذوزنقه متساوی الساقین زاویه های تند با هم و زاویه های باز با هم برابرند.
- نکته: فقط در ذوزنقه متساوی الساقین قطر ها با هم برابرند.
-
نکته: دو زاویه را مکمل گویند هر گاه مجموع آنها ۱۸۰ باشد.
- نکته: دو زاویه را متمم گویند هر گاه مجموع آنها ۹۰ باشد.
- نکته: یک زاویه را تمام صفحه گویند هر گاه برابر با ۳۶۰ درجه باشد.
- نکته: مجموع زاویه های داخلی هر مثلث ۱۸۰ درجه است.
مجموع زاویه های داخلی یک n ضلعی:
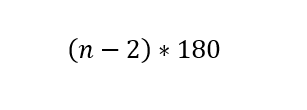
اندازه هر زاویه داخلی یک n ضلعی:
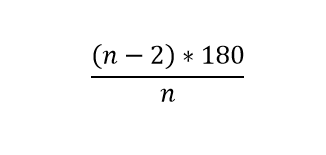
- اگر بخواهیم سطحی را فقط با یک نوع کاشی که به شکل چند ضلعی منتظم هستند کاشی کاری کنیم حتماً باید اندازه زاویه های چند ضلعی منتظم شمارنده ی ۳۶۰ باشند.
زاویه های خارجی
زاویه هایی که در هر راس یک چند ضلعی محدب بین یک ضلع و امتداد ضلع دیگر به وجود می آید، زاویه خارجی نامیده می شود.
- در هر مثلث اندازه هر زاویه ی خارجی با مجموع دو زاویه داخلی غیر مجاورش برابر است.
- مجموع زاویه های خارجی یک n ضلعی برابر ۳۶۰ است.
اندازه هر زاویه داخلی برابر:
با استفاده از اندازه ی زاویه ی خارجی اندازه هر زاویه داخلی یک ضلعی منتظم به صورت زیر محاسبه می شود
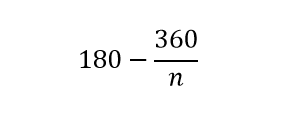
مجموعه آموزشی عینکی آمادهی هر کمکی برای موفقیت شما در ریاضی هست.
هر سوالی در ارتباط با چند ضلعی ها دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.
حتما بخوانید: عددهای صحیح و گویا






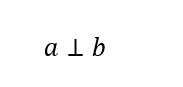
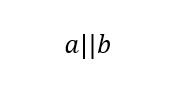




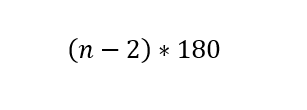
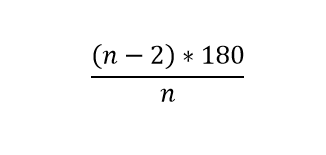
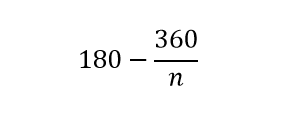
عالی ممنون❤
خواهش میکنم
کاشی کاری برای ریاضی هشتم
سلام
میخواستم اعداد اول بین ۶۰ تا ۹۰ رو به روش غربال کردن بگید پیدا نکردم تو سایت
سلام
روش غربال کردن رو به زودی توی دروس پایه هشتم مطرح می کنیم.
۲..۳..۵..۷..۱۱..۱۳….۱۷..۱۹…۲۳.۲۹..۳۱..۳۷…۴۱..۴۳..۴۷..۵۳..۵۹..۶۱….۶۷..۷۱..۷۳..۷۹….۱۰۱…۱۰۳….۱۰۷..۱۰۹…۱۱۳…۸۳…۸۹…۹۷..
اعداد اول از ۱تا۱۲۰