حل معادله درجه دو به روش ضربدری

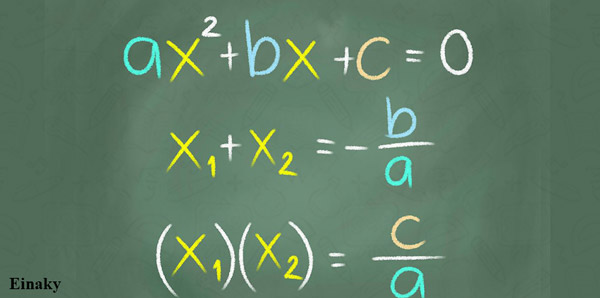
همانطور که می دانید برای حل معادله های درجه دو میتوان از روش تجزیه ، روش ریشه گیری، روش مربع کامل و روش دلتا استفاده کرد.

اما در این مقاله ” حل معادله درجه دو با استفاده از مجموع و حاصل ضرب ریشه ها یا روش ضربدری “، که روش جدیدی برای حل معادلات درجه دو می باشد را به شما آموزش خواهیم داد.

 حل معادله درجه دو با استفاده از مجموع و حاصل ضرب ریشه ها ، روشی بر مبنای آزمون و خطا است.  

این روش مشابه فاکتور گیری است با این تفاوت که تعداد حالت ها به نصف کاهش می یابد.
همچنین این روش برای معادله های درجه دومی که بتوان از آنها فاکتور گرفت مناسب می باشد.
دقت کنید که برای راحتی کار در معادله ax² +bx+c = 0 ، علامت a را مثبت در نظر می گیریم.

مراحل حل معادله درجه دو به روش ضربدری

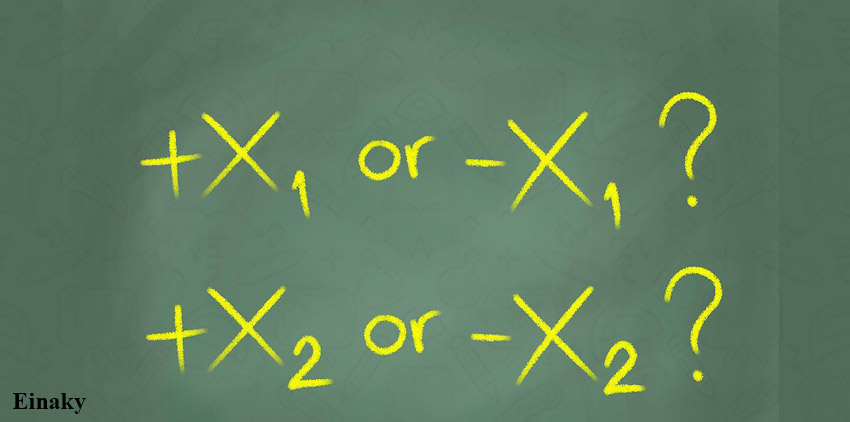
1- معادله درجه دوم دو ریشه دارد.

همانطور که میدانید در معادله درجه دو مجموع ریشه ها از رابطه (b/a-) و حاصل ضرب ریشه ها از رابطه (c/a) به دست می آید.

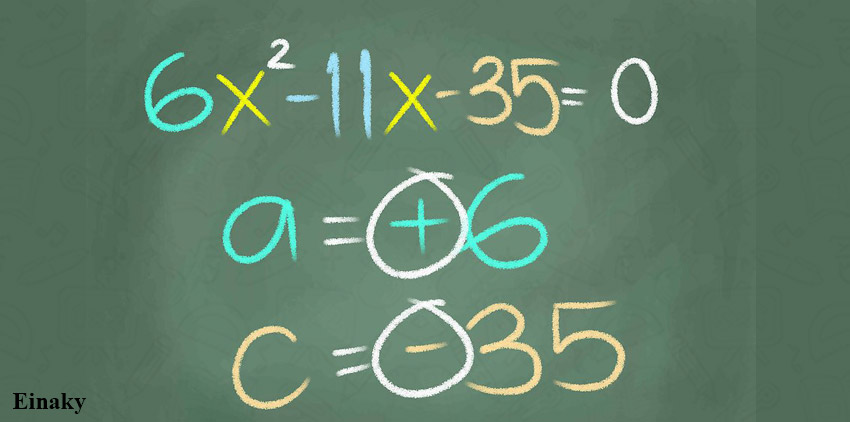
2- استفاده از قاعده علامت برای ریشه ها

برای اینکه تعداد انتخاب ها را کاهش دهیم میتوانید از قاعده زیر استفاده کنید:

اگر a و c مختلف العلامت باشند، هر دو ریشه نیز مختلف العلامت هستند.
به عنوان مثال در عبارت 6x² – 11x – 35 = 0 دو ریشه مختلف العلامت هستند چون a=6 و c=-35 است.

اگر a و c هم علامت باشند، دو ریشه حقیقی هم علامت هستند و بعداً میتوانیم تشخیص دهیم که هر دو مثبت یا هر دو منفی هستند.

اگر a و b مختلف العلامت باشند هر دو ریشه مثبت هستند.

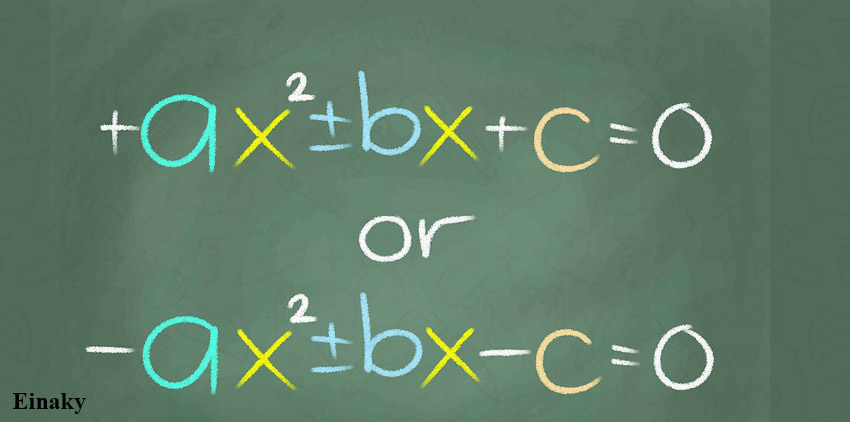
در عبارت 21x² – 23x + 6 = 0 هر دو ریشه حقیقی مثبت هستند.

در واقع از این روش نمیتوانیم برای  معادلات درجه دو که ریشه حقیقی ندارند (مثل 21x² – x + 6 = 0) استفاده کنیم.

اما میتوانیم بگوییم که اگر دو ریشه معادله حقیقی باشند، هر دو ریشه مثبت هستند.

اگر a و b هم علامت باشند هر دو ریشه منفی هستند.

برای مثال 15x² + 22x + 8 = 0 دو ریشه دارد که هر دو منفی هستند.

مجدد ذکر میکنیم این روش برای ریشه های مرکب جواب نمیدهد.

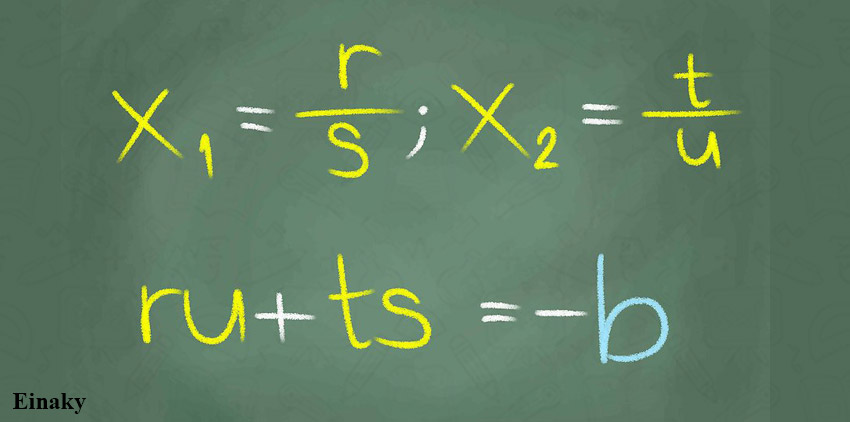
3- فرض کنید که تساوی درجه دوم دو ریشه حقیقی گویا دارد، ریشه ها را به صورت عبارت کسری  با مخرج مثبت در عبارت بیان میکنیم.

اگر ریشه ها r/s و t/u باشند پس جمع مورب  ru+ts=-b میباشد. عبارت ru+ts جمع ضربدری (یا اریب) نامیده می شود.

نکته: در این فرمول a را مثبت در نظر می گیریم، اگر a منفی باشد ru+ts=b میشود.

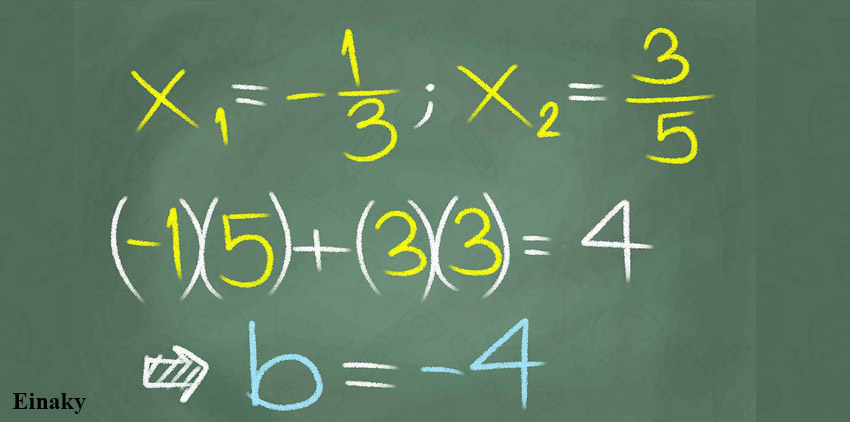
اگر دو ریشه حقیقی-1/3 و 3/5 باشد جمع اریب آنها 4 = -5 + 9 =  (-1)*(5) + (3)*(3) میشود.
معادله درجه دوم برای این عبارت 15x² – 4x – 3 = 0 میباشد.

نکته: علامت b مخالف جمع اریب مورد انتظار میباشد.

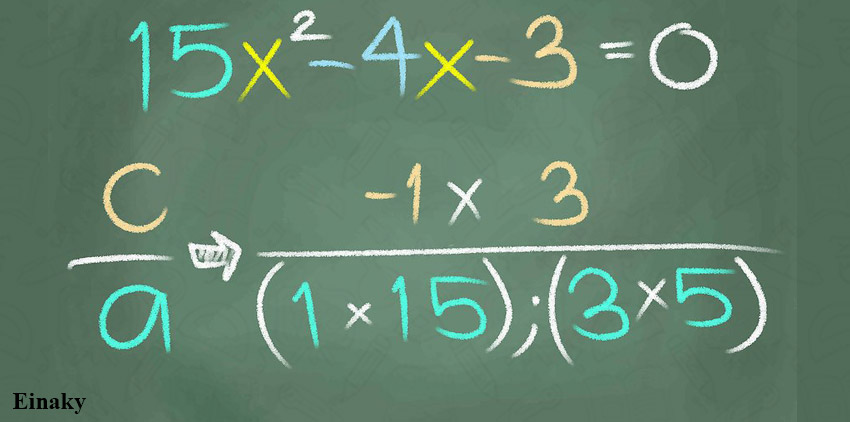
4- از a و c فاکتور بگیرید.

تمام کسر هایی که در آنها صورت کسر برابر r.t =c و مخرج کسر برابر s.u =a را بنویسید.

با استفاده از قاعده علامت ها، علامت درست را برای کسر ها در نظر بگیرید.

در غیر این صورت اگر ریشه ها هم علامت نیستند نیازی به بررسی {1/3, -3/5} و {-1/3, 3/5} نیست.
اگر جمع اریب یا ضربدری یکی از دو جفت ریشه ها مقدار صحیح داشته باشد اما علامت آن اشتباه باشد پس جفت کسر دیگر جواب معادله است.

دقت کنید که فقط یکی از حالت ها جواب معادله درجه دو خواهد بود.

5- جمع اریب جفت کسرها را بررسی کنید.

اگر جمع اریب مساوی b- نباشد پس جواب است.

اگر جمع اریب مساوی b+ باشد، مخالف جواب است .

اگر جمع اریب b- یا b نباشد ریشه های معادله درجه دوم گنگ یا مرکب است و باید از روش های دیگر ریشه های آن را به دست آورد.

حتما بخوانید: انواع اتحاد جبری ریاضی نهم