
نکته: در ریاضیات برای نام گذاری شکل ها از حروف انگلیسی استفاده میکنیم.
نکته: در هر مثلث مجموع اندازه های دو ضلع، از اندازه ضلع سوم بیشتر است.
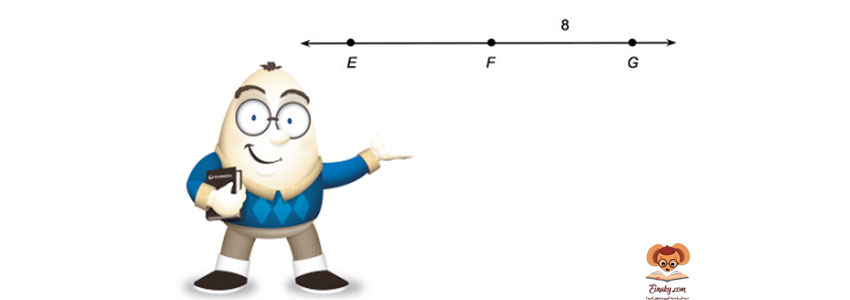
نکته: اگر n نقطه روی یک خط در نظر بگیریم، تعداد پاره خط ها از رابطه زیر به دست می آید:
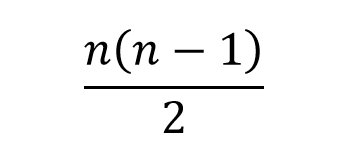
مثال: اگر تعداد نقاط روی خط 3 باشد، تعداد پاره خط ها برابر است با 6 (کافی است در رابطه بالا به جای n مقدار 3 را قرار دهیم.)
نکته: اگر روی یک خط راست n نقطه در نظر بگیریم، آنگاه تعداد نیم خط ها برابر با ۲n است.
در مثال قبل تعداد نیم خط ها برابر 6 خواهد بود.
خط: از کنار هم قرار گرفتن بی شمار نقطه ایجاد می شود.
انواع خط:خط راست، خط شکسته، خط منحنی
نکته: از یک نقطه بی شمار خط می گذرد.
نکته: از دو نقطه فقط یک خط راست می گذرد.
نکته: از دو نقطه بی شمار خط منحنی و بی شمار خط شکسته می گذرد.
نیم خط: هرگاه قسمتی از یک خط را از یک طرف با یک نقطه محدود نماییم، یک نیم خط حاصل می شود.
پاره خط: هر گاه بخشی از یک خط را که بین دو نقطه از آن خط می باشد، محدود نماییم، پاره خط ایجاد می شود.
نکته: در هندسه از علامت || که نشان دهنده دو خط موازی است، برای نشان دادن موازی بودن دو خط استفاده می شود.
نکته: اندازه پاره خط AB برابر است با اندازه پاره خط BA.
نکته: برای جمع دو پاره خط ، آن ها را به دنبال هم قرار می دهیم و برای تفریق دو پاره خط آن ها را روی هم قرار می دهیم تا حاصل مشخص شود.

برای نام گذاری یک زاویه طبق قرار داد هایی که برای نمایش نقاط، نیم خط ها و… داشتیم، می توانیم راس را با حروف بزرگ انگلیسی و دو ضلع آن ( دو نیم خط) را با حروف کوچک انگلیسی نمایش دهیم.
زاویه نیم صفحه(تخت): 180 درجه
زاویه راست(قائمه): 90 درجه
زاویه تند(حاده): کمتراز 90 درجه
زاویه باز(منفرجه): بین 90 و 180 درجه
زاویه مقعر(کاو): هر زاویه ای که اندازه آن بیشتر از 180 درجه و کمتر از 360 درجه باشد.
زاویه محدب(کوژ): هر زاویه ای که کمتر از 180 درجه باشد.
نیمساز: نیمساز خطی است که شروع آن راس زاویه است و زاویه را به دو زاویه برابر تقسیم می کند.
دو زاویه متمم: اگر مجموع اندازه های دو زاویه برابر 90 باشد، دو زاویه متمم یکدیگر نامیده می شوند.
مثال: دو زاویه 40 درجه و 50 درجه متمم هم هستند زیرا مجموع آنها برابر 90 درجه است: 40+50=90
دو زاویه مکمل: اگر مجموع اندازه های دو زاویه برابر 180 باشد،دو زاویه مکمل یکدیگر نامیده می شوند.
مثال: دو زاویه 120 درجه و 60 درجه مکمل هم هستند زیرا مجموع آنها 180 درجه است:120+60=180
نکته: در هر مثلث، مجموع زاویه های داخلی برابر 180 درجه است.

مثلث متساوی الاضلاع: مثلثی که سه ضلع آن با هم مساوی است.
مثلث متساوی الساقین: مثلثی که دو ضلع آن با هم مساوی اند.
مثلث قائم الزاویه: مثلثی که یک زاویه 90درجه دارد.
مثلث مختلف الاضلاع: مثلثی که اضلاع آن با هم مساوی نیستند.
دسته بندی مثلث ها با توجه به اندازه زاویه ها
1- مثلث هایی که هر سه زاویه آنها تند است.
2- مثلث هایی که یک زاویه راست دارند.
3- مثلث هایی که یک زاویه باز دارند.

چند ضلعی هایی که هیچ کدام از زاویه های آن ها بزرگتر از ۱۸۰ درجه نباشد، چند ضلعی محدب نامیده می شود.
مثال: مثلث متساوی الاضلاع، یک چند ضلعی محدب است زیرا تمام زاویه های آن کوچکتر از 180درجه است(هر زاویه آن 60درجه است.)
چند ضلعی هایی که دست کم یک زاویه بزرگتر از ۱۸۰ درجه داشته باشند، چند ضلعی مقعر می گویند.
به چند ضلعی هایی که همه ضلع هایشان با هم و همه زاویه هایشان نیز با هم مساوی باشند، چند ضلعی منتظم گفته می شود.
هر چند ضلعی منتظم یک چند ضلعی محدب است.
نکته: مجموع زاوی های داخلی n ضلعی برابر است با:
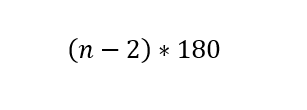
مثال: مجموع زاویه های داخلی یک 5 ضلعی را به دست آورید:
(5-2)*180=540
نکته: اندازه هر زاویه داخلی n ضلعی منتظم برابر :
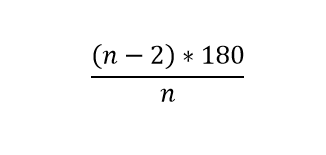
مثال: اندازه هر زاویه داخلی یک 5 ضلعی منتظم را به دست آورید؟
(5-2)*180=540/5=18
انتقال: اگر یک شکل را بدون تغییر جهت روی صفحه حرکت دهیم تا به مکان دیگری برود، به این عمل انتقال و شکل حاصل را انتقال یافته شکل اولیه می گوییم.
نکته: وقتی شکلی را روی صفحه انتقال می دهیم، تصویر به دست آمده مساوی و هم جهت با شکل اولیه است.
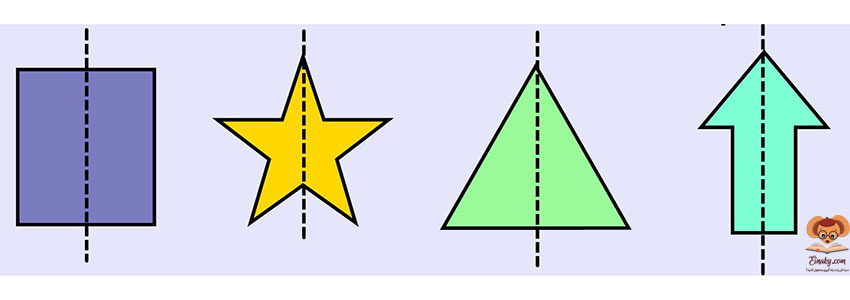
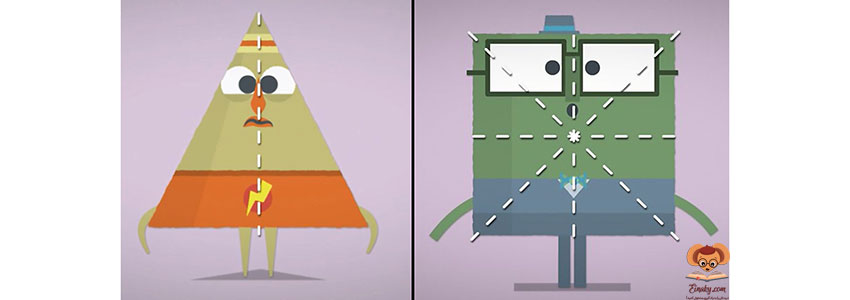
تقارن محوری(تقارن نسبت به خط): اگر قرینه تمام نقاط شکل A را نسبت به خط d مشخص کنیم، آنگاه شکلی مانند B حاصل می شود که آن را قرینه شکل A نسبت به خط تقارن D می نامیم.
نکته: وقتی قرینه شکلی را نسبت به یک خط پیدا می کنیم، تصویر به دست آمده مساوی آن شکل است اما جهت آن تغییر می کند.
دوران: اگر شکل A را حول یک نقطه ثابت بچرخانیم و شکل جدید را B بنامیم آنگاه شکل B دوران یافته شکل A است، این عمل را دوران و نقطه ثابت را مرکز دوران می نامیم.
دوران به اندازه ۱۸۰: در دوران به اندازه ۱۸۰ درجه، در جهت حرکت عقربه های ساعت و یا خلاف آن مهم نمی باشد و در هر دو حالت شکل های یکسان به دست می آید.
نکته: برای مشخص کردن دوران یافته یک چند ضلعی حول مرکز دوران به اندازه ۱۸۰ درجه کافی است راس های چند ضلعی را به مرکز دوران وصل کنیم و آن ها را به همان اندازه امتداد می دهیم تا راس های چند ضلعی دوران یافته مشخص شود.
دوران به اندازه۹۰: در دوران به اندازه ۹۰ درجه جهت دوران مهم است.
نکته: برای مشخص کردن دوران یافته یک چند ضلعی حول مرکز دوران به اندازه ۹۰ درجه کافی است، راس های چند ضلعی را به مرکز دوران وصل کنیم و آنها را به اندازه ۹۰ درجه دوران دهیم تا راس های چند ضلعی دوران یافته مشخص شود.

اگر بتوانیم شکلی را با یک یا چند تبدیل در صفحه بر شکل دیگری در صفحه منطبق کنیم، می گوییم این دو شکل با هم همنهشت هستند.
نکته: در دو شکل هندسی همنهشت، اجزای متناظر دو به دو با هم برابرند، تساوی اجزای متناظر را هم میتوان روی شکل مشخص کرد و هم میتوان با علامت تساوی به زبان ریاضی نوشت.
مجموعه آموزشی عینکی آمادهی هر کمکی برای موفقیت شما در ریاضی هست.
همچنین برای آشنایی با نمونه سوالات بیشتر میتوانید فیلم آموزش فصل چهارم ریاضی هفتم را مشاهده کنید.
هر سوالی در ارتباط با هندسه و استدلال ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد
دریافت فایل pdf هندسه و استدلال ریاضی هفتم
حتما بخوانید: جبر و معادله (فصل سوم ریاضی هفتم)
سلام خانم دوستی
بسیار عالی
پایدار باشید و سربلند
سلام
خواهش میکنم ممنون از حضورتون در سایت عینکی
خیلی خوب و به صورت خلاصه توضیح داداه بودی و البته سوال هایی که بلد نبودم را هم یا گرفتم😁
خیلی خوب و به صورت خلاصه توضیح داداه بودی و البته سوال هایی که بلد نبودم را هم یا گرفتم😁
سلام
ب.م.م و ک.م.م رو چطور به دست بیارم؟