پیدا کردن محل تلاقی دو خط

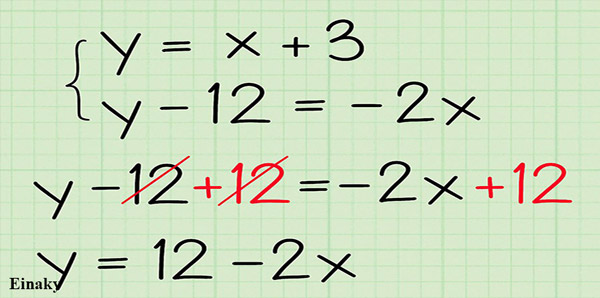
همانطور  که میدانید یک خط در دستگاه مختصات با مجموعه ای از نقاط مشخص می شود.

وقتی دو خط با هم تلاقی دارند یعنی مختصات نقطه تلاقی باید در هر دو خط صدق کند.

در این مقاله روش هایی برای بدست آوردن محل تلاقی دو خط خواهیم آموخت. در ادامه مطلب با عینکی همراه باشید.

 

بدست آوردن محل تلاقی دو خط راست

۱- معادله هر دو خط را به صورت استاندارد بنویسید.

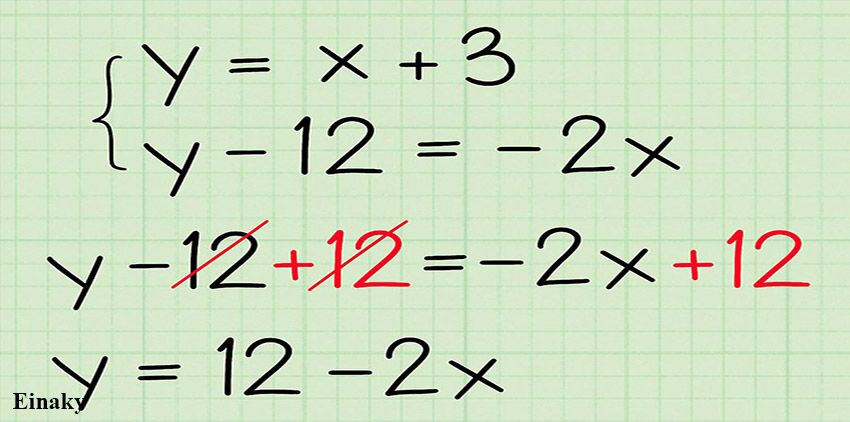
برای اینکه معادله خط به صورت استاندارد نوشته شود باید y را تنها در یک طرف تساوی بنویسید.

اگر به جای y از (f(x یا (g(x استفاده می کنید، همانند y باید آنها را تنها در یک طرف تساوی نوشت. 
نکته: دقت داشته باشید  با جابه جا کردن عبارت ها در طرفین تساوی، علامت آنها نیز عوض می شود.

سوال: دو خط که در یک نقطه یکدیگر را قطع کنند چه نام دارد؟ دو خط متقاطع

۲- طرف راست معادله خط را مساوی طرف چپ قرار دهید.

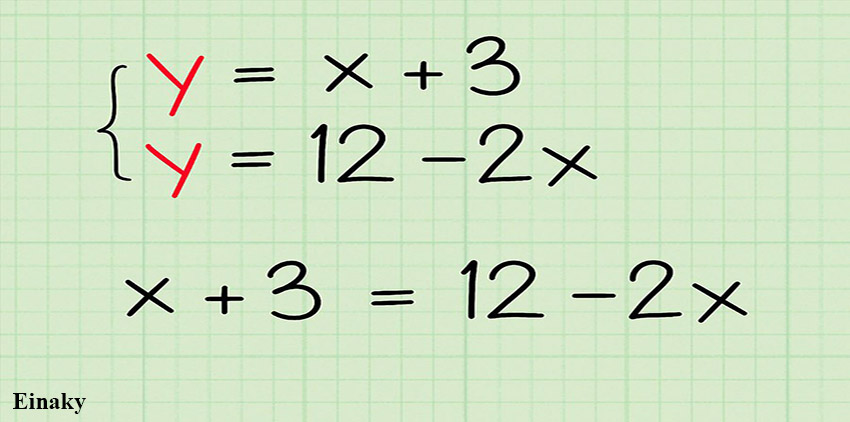
هدف پیدا کردن نقطه ای است که در هر دو معادله خط صدق کند. این نقطه همان مکانی است که دو خط یکدیگر را قطع می کنند.

دقت داشته باشید که سمت چپ هر دو معادله خط تنها یک y دارد و با هم مساوی هستند، بنابر این سمت راست هر دو معادله خط نیز با هم برابر است.

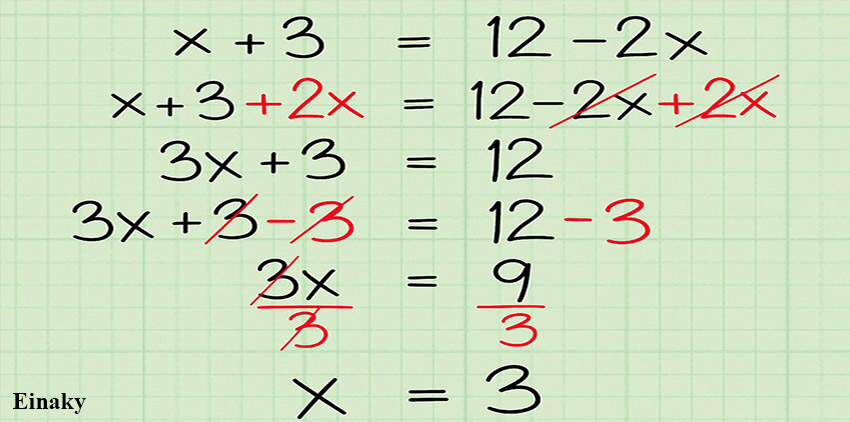
۳- مقدار x را در معادله خط بدست آورید.

معادله جدید فقط یک متغیر x دارد، که با استفاده از جبر مقدار آن را بدست می آوریم.

مثال:

• 12-2x=3+x

به هر دو طرف معادله عبارت 2x را اضافه کنید داریم:

• 3x+3=12

از هر دو طرف معادله مقدار 3 را کم می کنیم داریم:

• 3x=9

در طرف معادله را بر 3 تقسیم می کنیم داریم:

• 3=x

۴- با استفاده از مقدار بدست آمده برای x مقدار y را بدست آورید.

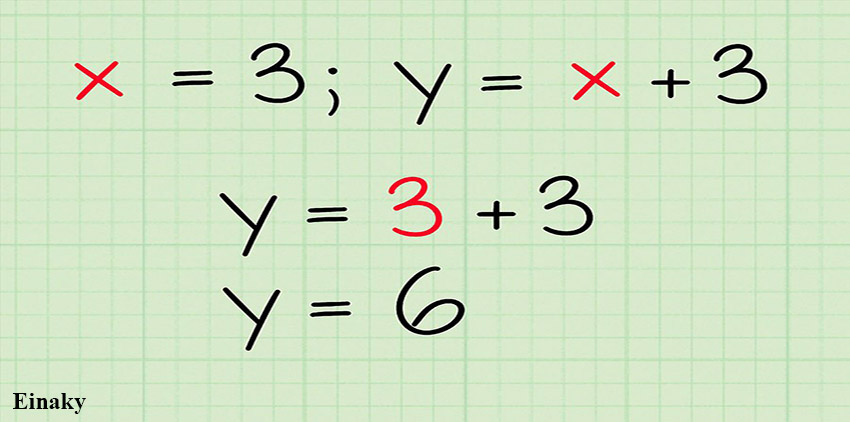
یکی از معادله خط ها را انتخاب کرده و در آن هر جا متغیر x وجود دارد به جای آن مقدار بدست آمده برای x را قرار دهید.

مثال:

اگر x+3=y   ,  x=3  باشد داریم:

• y=3+3
• y=6

۵- پاسخ خود را بررسی کنید. 

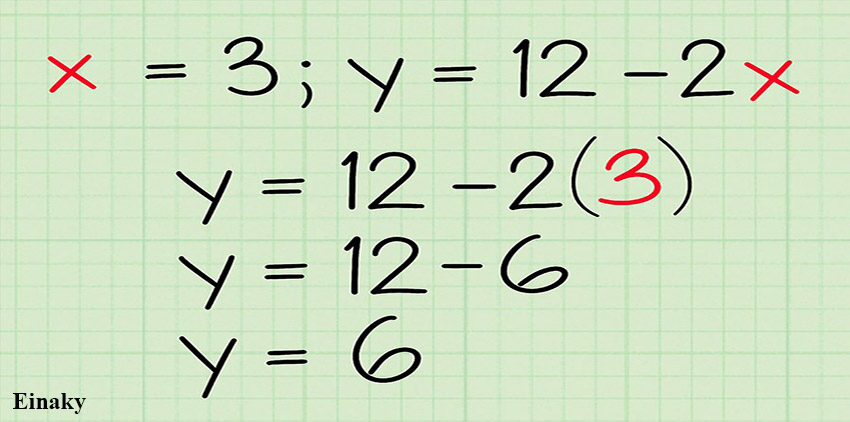
پیشنهاد می شود برای اطمینان از درستی پاسخ، مقدار x  را در معادله خط دوم نیز قرار داده و مقدار y را بدست آورید، اگر دو مقدار متفاوت برای y بدست بیاید، به این معناست که یکی از مراحل را به اشتباه محاسبه کرده اید.

مثال:

اگر x=3   , y=12-2x باشد داریم:

• y=12-(3)2
• y=6

از آنجا که مقدار y برای هر دو معادله خط یکسان بدست آمد پس اشتباهی در حل معادله رخ نداده است.

۶- مقدار x و y را به عنوان مختصات محل تلاقی دو خط بنویسید.

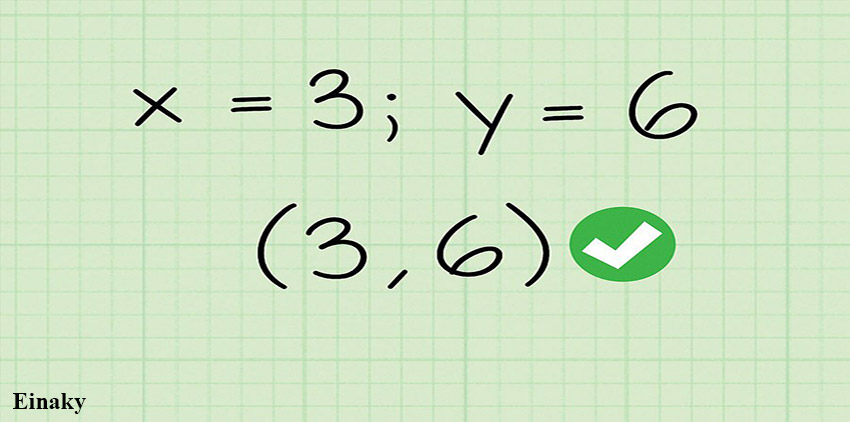
مقدار بدست آمده برای  x و y  همان نقطه تلاقی دو خط هستند. برای این مثال مختصات محل تلاقی برابر (3,6) است.

۷- بدست آوردن مقادیر غیر معمول برای متغیر ها

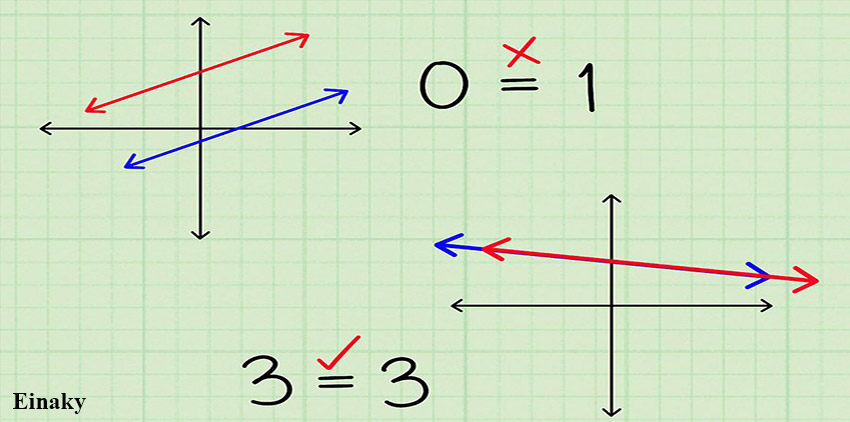
در بعضی از معادله ها، امکان ساده کردن معادله و بدست آوردن مقدار x غیرممکن است، این به معنای این نیست که شما معادله را اشتباه حل کرده اید.

اگر دو خط موازی باشند و یکدیگر را قطع نکنند. در این مواقع ممکن است دو طرف معادله خط با هم مساوی نشود (مثلاً 0=1). در این مواقع برای جواب میتوانیم بنویسیم دو خط متقاطع نیستند و معادله جواب حقیقی ندارد.

اگر هر دو معادله، مربوط به یک خط باشد، دو خط یکدیگر را در بی نهایت نقطه قطع می کنند. در این صورت برای جواب میتوانیم بنویسیم دو خط یکی هستند.

بدست آوردن محل تلاقی خط با معادله درجه 2

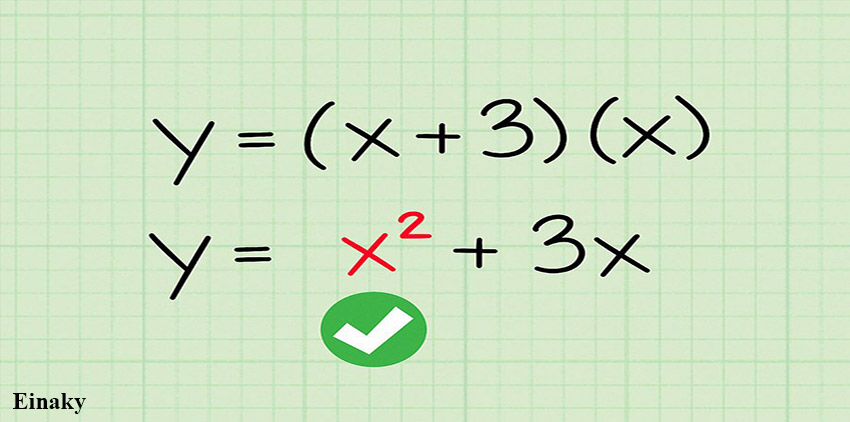
1- در معادله درجه 2، بزرگترین توان متغیر 2 است و نمودار این توابع به صورت منحنی می باشد.

برای این معادله ها، 0،1 یا 2 جواب بدست می آید.

بررسی کنید آیا معادله درجه 2 است یا خیر؟ به عنوان مثال در عبارت  x+3)(x)=y) اگر دو پرانتز را در هم ضرب کنیم به معادله درجه دوم y=3x+x² می رسیم.

این بخش نشان میدهد که چگونه 0, 1،یا 2 راه حل برای حل مساله بیابید.

در معادله های درجه 2 متغیر x یا y حتما توان 2 دارند.

2- در هر دو معادله درجه 2، y را تنها در یک طرف معادله قرار دهید.

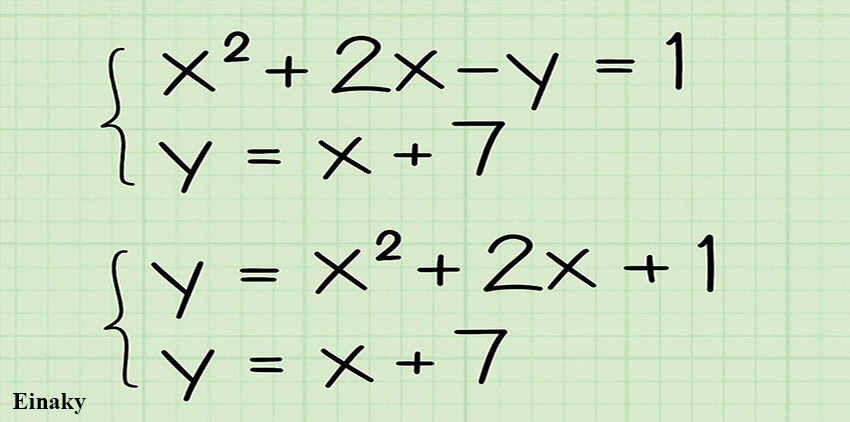
به عنوان مثال اگر دو معادله خط به صورت زیر داشته باشیم:

• 1-=x²+2x-y
• 7+y=x

بعد از مرتب شدن خواهیم داشت:

• y=1+2x+x²
• 7+y=x

۳- دو معادله را با هم ترکیب کنید.

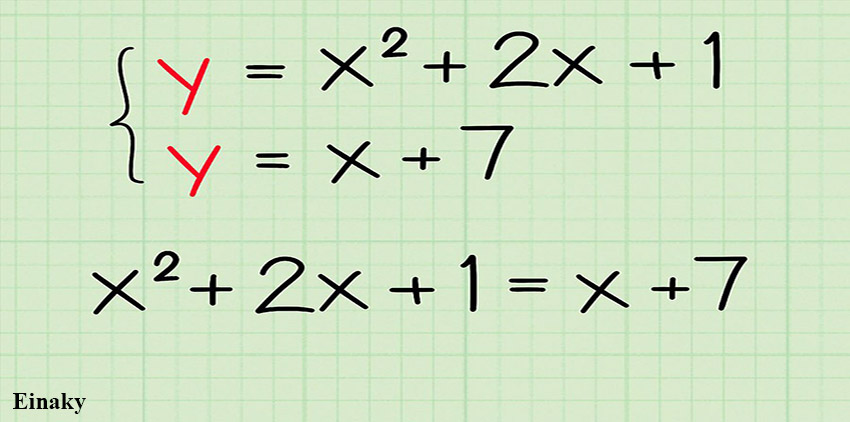
برای اینکه مقدار y را بدست آوریم کافی است طرف راست دو معادله درجه دو را مساوی هم قرار دهیم (دقت کنید که سمت چپ هر دو معادله برابر y است.)

در مثال ذکر شده داریم:

• 1+2x+x²=7+x

4-  معادله جدید را مرتب کرده و آن را مساوی صفر قرار دهید.

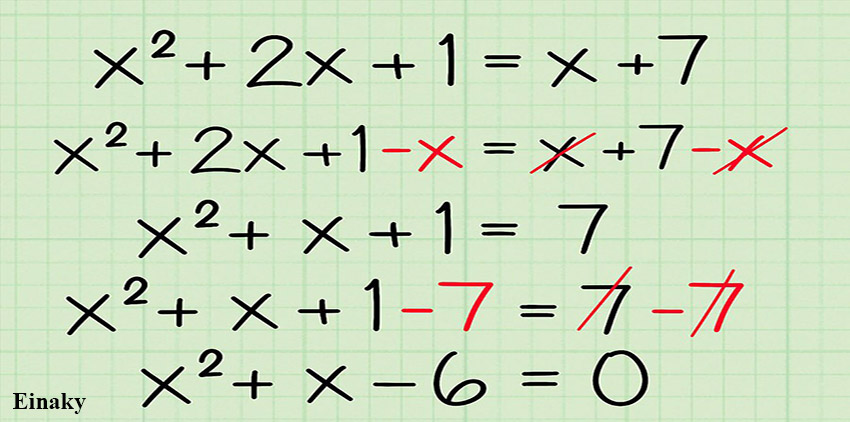
در معادله قبل از هر دو طرف معادله  x را کم کنید داریم:

• 1+1x+x²=7

از هر دو طرف معادله عدد 7 را کم کنید داریم:

• 0=6-x+x²

۵- معادله درجه دو را حل کنید.

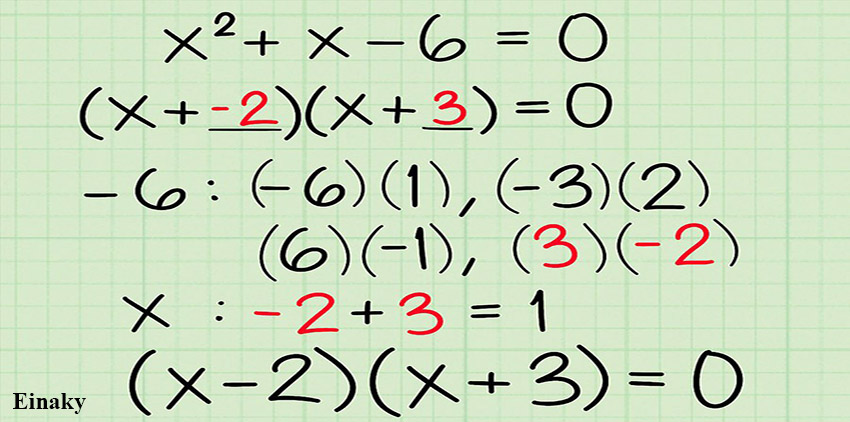
زمانی که معادله را برابر با صفر قرار می دهیم، با استفاده از اتحادها و یا روش دلتا می توانیم معادله را حل کنیم که معمولاً ساده ترین راه را انتخاب میکنیم.

در مثال بالا از اتحاد جمله مشترک برای تجزیه عبارت درجه دوم استفاده می کنیم.

برای تجزیه عبارت با استفاده از اتحاد جمله مشترک باید دو پرانتز در نظر بگیریم که جمله مشترک یعنی x در هر دو آنها قرار داشته باشد.

سپس دو عدد در نظر می گیریم که حاصل ضرب آنها برابر جمله آخر و حاصل جمع آنها برابر با جمله دوم باشد.

در مثال قبل داریم:

• 0=(x-2)(x+3)

۶- حل معادله به روش های مختلف

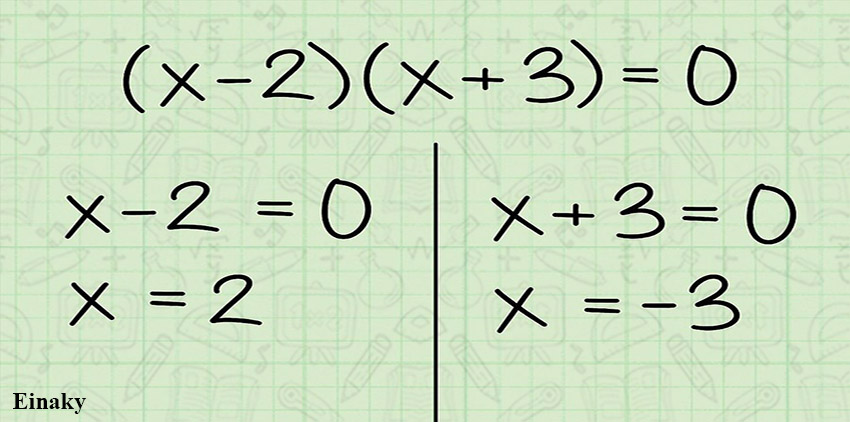
دقت داشته باشید که برای حل معادله درجه دو میتوانید از روش های مختلف استفاده کنید اما در همه روش ها باید یک مقدار یکسان برای x بدست بیاید.

در این مثال اگر عبارت  0=x-2  را حل کنیم برای x مقدار 2 بدست می آید، همچنین  با حل 0=x+3  مقدار 3- برای x بدست می آید.

در صورت حل معادله درجه 2 با استفاده از روش دلتا نیز همین دو مقدار برای x بدست می آید.

۷- حل معادلات خط با صفر یا یک جواب

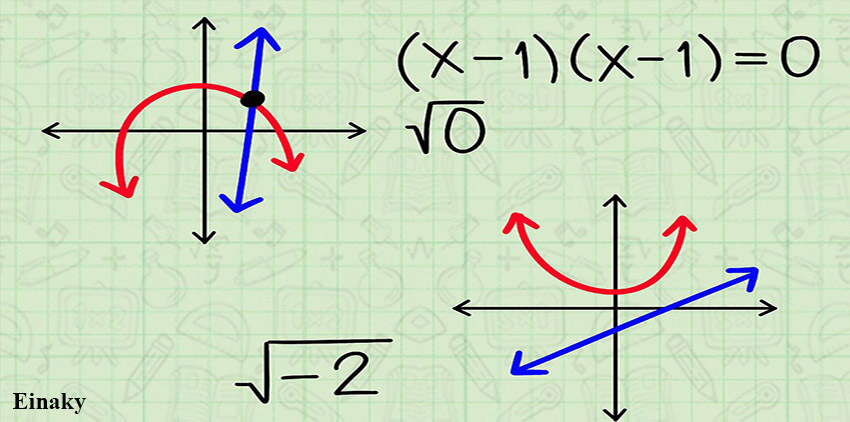
برای تشخیص خطوطی که همدیگر را قطع نمیکنند و یا فقط در یک نقطه همدیگر را قطع می کنند: 

اگر معادله دارای یک ریشه باشد (مثال ((x-1)(x-1) = 0))، کافی است  مقدار یکی از آنها را بدست آورده و در معادله جایگزین کنیم.

اگر معادله دارای ریشه حقیقی نباشد: در این موارد هیچ مقدار حقیقی برای x بدست نمی آید و یا اینکه عبارت زیر رادیکال یک مقدار منفی است که همانطور که میدانید مقادیر منفی زیر رادیکال با فرجه زوج تعریف نشده اند.

۸- مقدار x را در معادله اصلی جایگزین کنید.

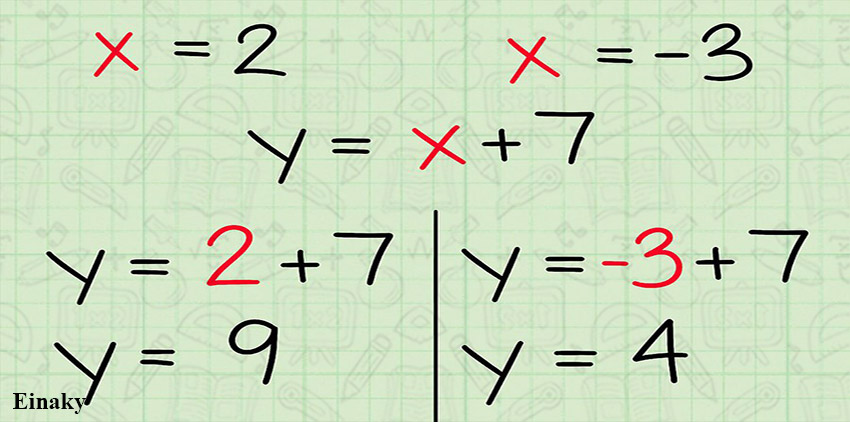
بعد از بدست آوردن مقدار x کافی است آن را در یکی از دو معادله جایگذاری کرده و مقدار y را بدست آورید.( برای  اطمینان بیشتر می توانید مقدار x را در معادله دوم نیز قرار داده و مقدار y را محاسبه کنید.)

۹- مختصات نقطه تلاقی دو خط  را بنویسید.

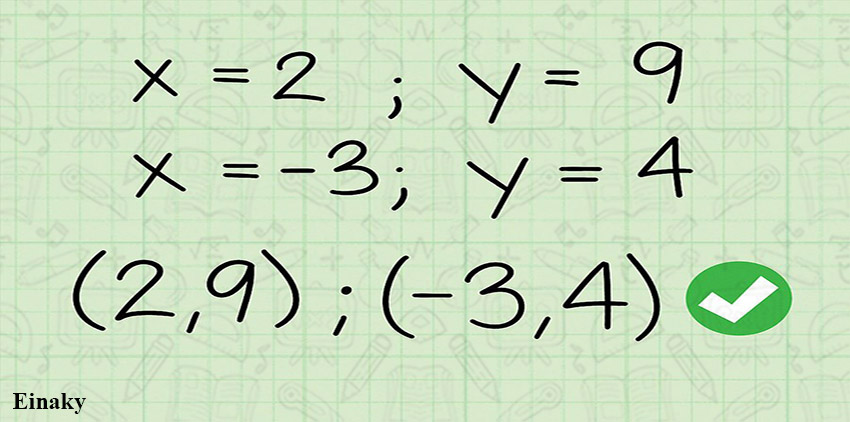
مقدار x و y بدست آمده را به صورت مختصاتی بنویسید.

 

حتما بخوانید: چطور میانه ، مد و میانگین را به دست آوریم؟