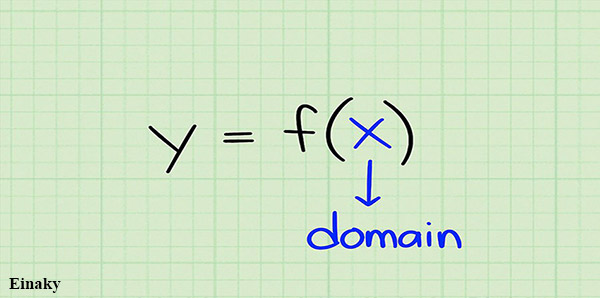
دامنه تابع مجموعه ای از اعداد است ، که میتواند در تابع به جای x قرار بگیرند.
مجموعه اعداد y برد تابع نامیده می شود.
برای به دست آوردن دامنه توابع رادیکالی، توابع چند جمله ای، توابع کسری و … با عینکی همراه باشید.
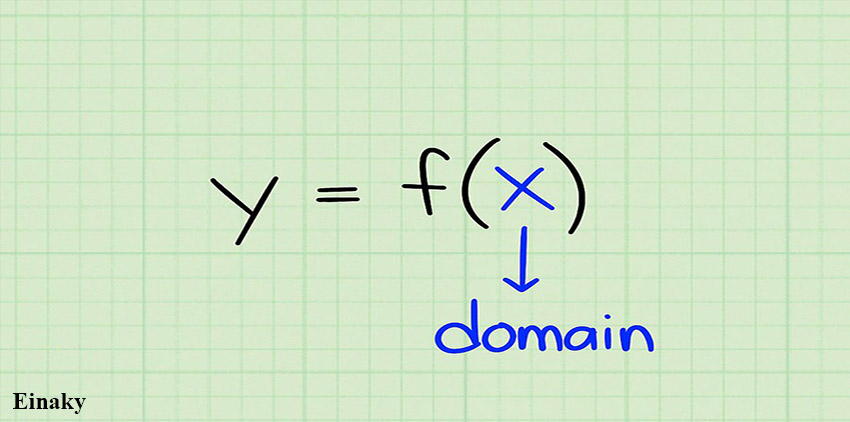
دامنه شامل تمام مقادیری است که به عنوان ورودی به یک تابع داده می شود و برد مجموعه تمام مقادیری است که به عنوان خروجی از تابع گرفته می شود.
به عبارت دیگر دامنه مجموعه ای از مقادیر x می باشد که میتواند در تابع قرار گرفته و مقدار y را تولید کند.
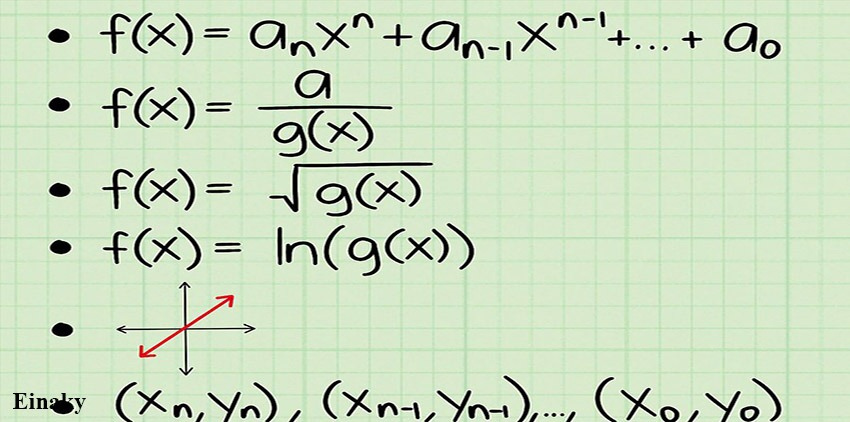
روش پیدا کردن دامنه برای توابع مختلف متفاوت است، قبل از اینکه دامنه یک تابع را به دست آورید باید نوع تابع را تعیین کنید.
دامنه توابع چند جمله ای غیر رادیکالی و کسری
دامنه این نوع توابع مجموعه اعداد حقیقی یا R است.
دامنه توابع کسری
برای پیدا کردن دامنه توابع کسری ، مخرج را مساوی با صفر قرار داده و با حل معادله مقادیر X را به دست می آوریم.
دامنه توابع رادیکالی
برای به دست آوردن دامنه توابع رادیکالی ، کافی است عبارت زیر رادیکال را بزرگتر از صفر قرار داده و معادله را حل کنیم، مقادیر به دست آمده برای X دامنه تابع را مشخص می کند.
برای به دست آوردن دامنه توابع لگاریتمی، کافی است عبارت موجود در پرانتز جلوی لگاریتم را بزرگتر از صفر قرار داده و معادله را حل کنید.
قسمت هایی از نمودار که بر روی محور X ها منطبق می شوند دامنه آن را مشخص می کنند.
دامنه توابع زوج مرتبی
دامنه این توابع مقادیر مولفه های اول یا X ها می باشد.
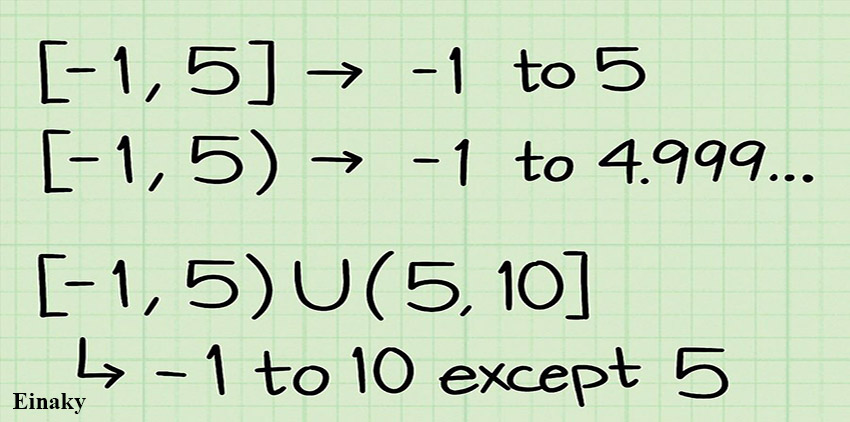
3- دامنه تابع را به درستی نمایش دهید.
به دست آوردن دامنه تابع ساده است، اما مهترین نکته در تعیین دامنه توابع ، نحوه نمایش و یا نوشتن آن است.
به عنوان مثال در (1,5-] دامنه بین 1- و 5 میباشد.
به عنوان مثال اگر دامنه مجموعه اعداد بین 1- تا 10 باشد اما 5 جز این دامنه نباشد، دامنه تابع را به این صورت بیان می کنیم:
[5,10) [-1,5) U
البته توجه داشته باشید که برای نماد بی نهایت باید از علامت پرانتز استفاده کنید نه براکت.
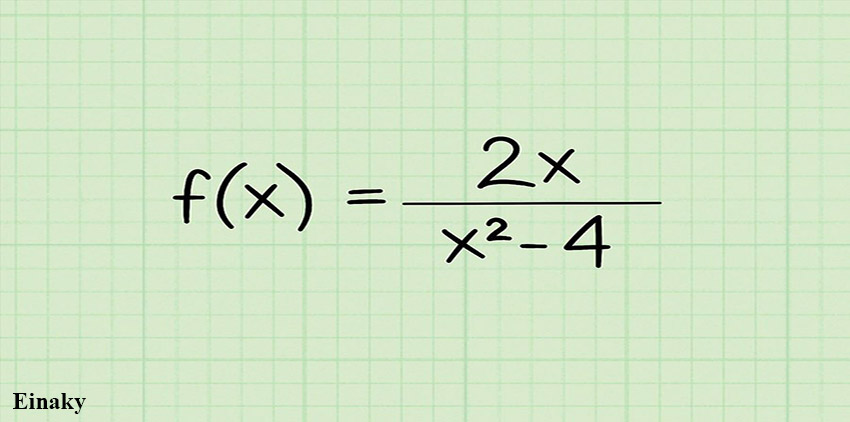
1- به عنوان مثال در اینجا دامنه تابع (f(x) = 2x/(x2 – 4 را به دست می آوریم.
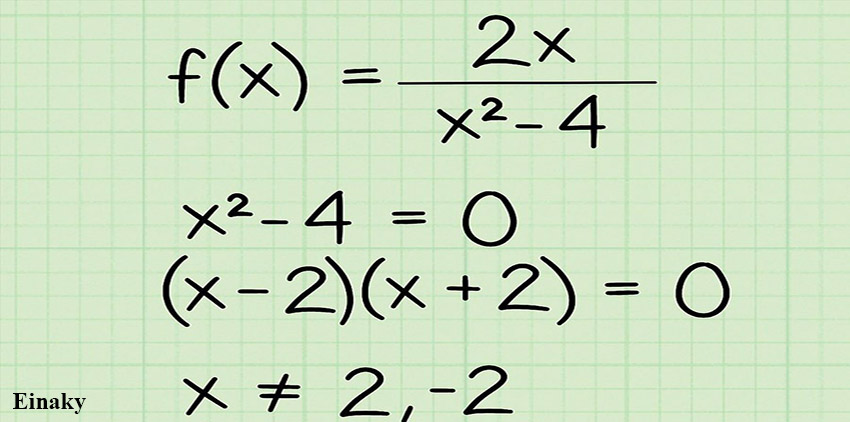
2- برای به دست آوردن دامنه توابع کسری باید عبارت مخرج را مساوی صفر قرار دهید، زیرا مقدار مخرج هیچگاه نباید صفر شود.
(f(x) = 2x/(x2 – 4
x2 – 4 = 0
x – 2 )(x + 2) = 0)
(x ≠ (2, – 2
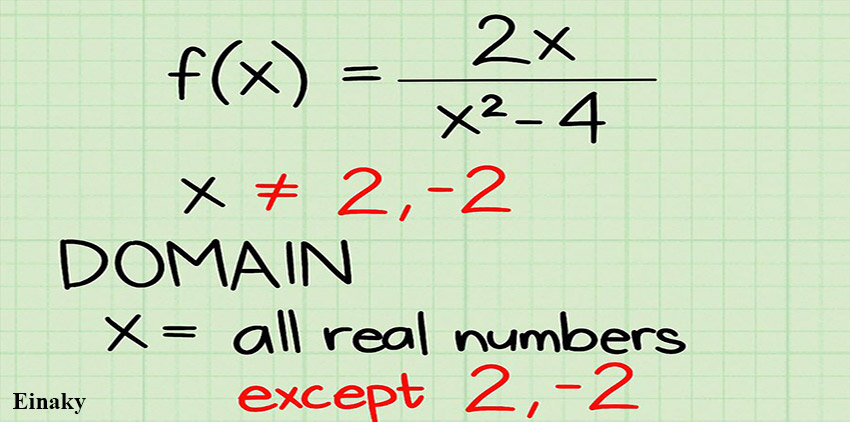
3- در این مثال دامنه شامل مجموعه همه اعداد حقیقی به جز 2 و -2 است.
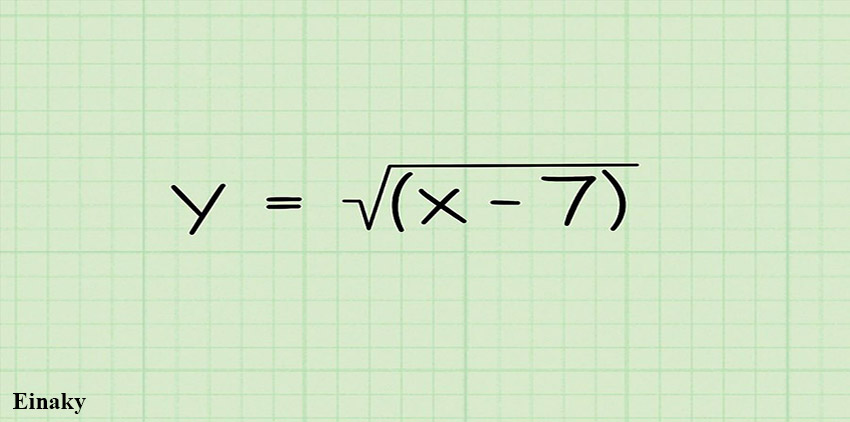
1- در این مثال میخواهیم دامنه تابع (Y =√(x-7را به دست آوریم.
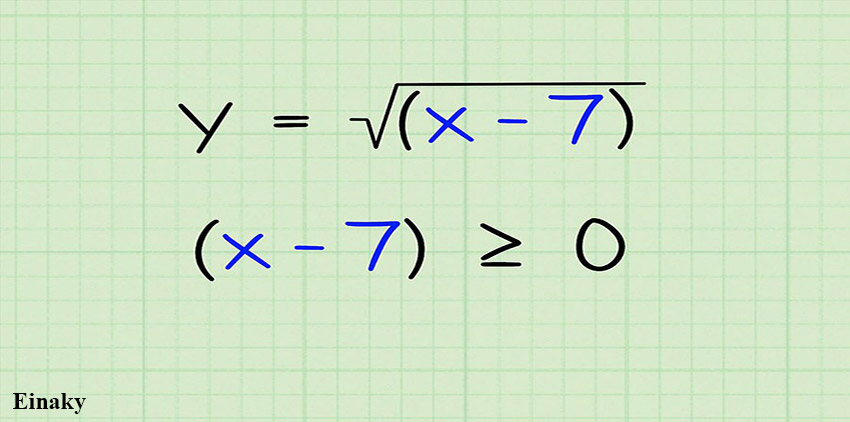
2- عبارت زیر رادیکال را بزرگتر یا مساوی صفر قرار می دهیم، دقت کنید که اعداد منفی ریشه دوم ندارد.
x-7 ≧ 0
نکته : از این روش میتوانید برای تمامی عبارت های رادیکالی با فرجه زوج استفاده کنید، اعداد منفی برای تمام رادیکال ها با فرجه زوج ریشه ندارند.
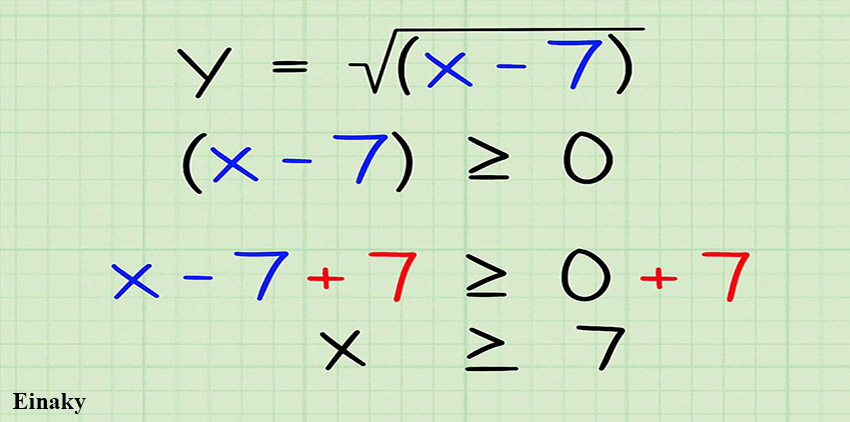
3- متغیر را به یک طرف معادله انتقال دهید
X را در سمت چپ معادله قرار داده و به هر دو طرف معادله عدد 7 را اضافه کنید. این کار را برای این انجام می دهیم که X به تنهایی در سمت چپ قرار بگیرد.
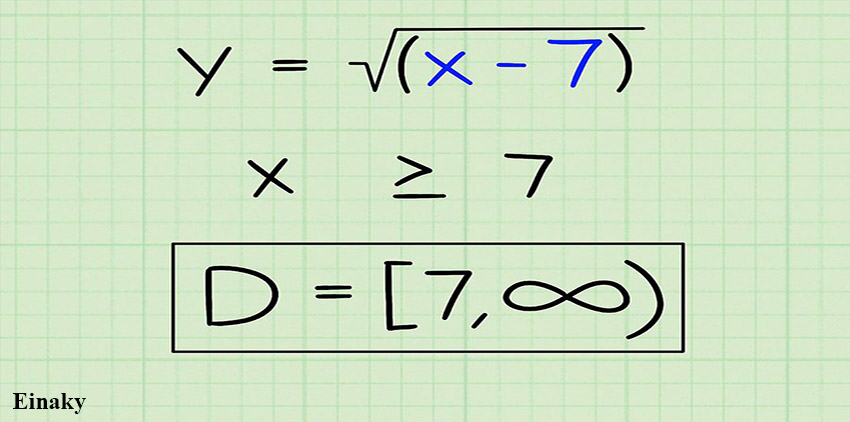
4- دامنه تابع رادیکالی را به درستی بیان کنید.
دامنه تابع برابر (∞,D = [7
دقت کنید که دامنه برابر اعداد بزرگتر یا مساوی 7 است پس عدد 7 عضو دامنه است و آن را با براکت نشان می دهیم.
در سمت راست عبارت بی نهایت قرار دارد که همانطور که گفته شد باید با علامت پرانتز نشان داده شود.
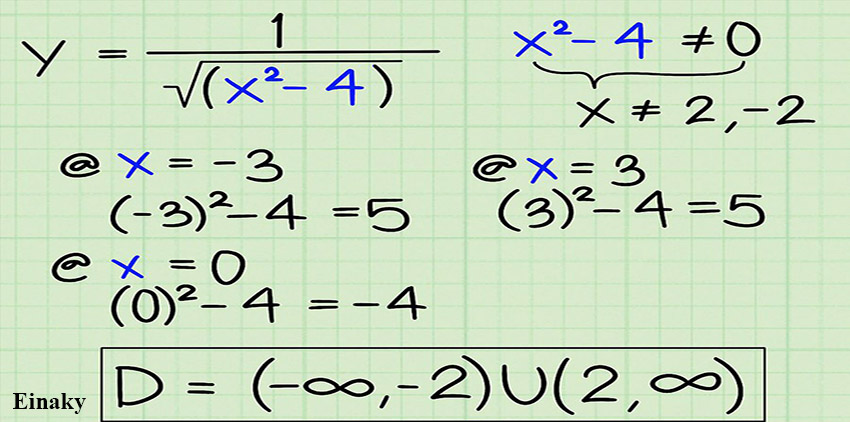
به عنوان مثال برای دامنه تابع (Y = 1/√( ̅x2 -4 وقتی مخرج را بزرگتر یا مساوی صفر قرار می دهید مقادیری که برای X به دست می آید (x ≠ (2, – 2
حالا باید اعداد کمتر از 2- (به عنوان مثال 3-) را به جای X قرار دهیم و بررسی کنیم آیا حاصل مقداری بزرگتر از صفر است یا خیر:
حال اعداد بین 2- و 2 را بررسی کنید.(صفر را قرار دهید.)
پس اعداد بین 2- و 2 جواب ندارند.
حال اعداد بیشتر از 2 مانند 3 را بررسی کنید.
پس اعداد بیشتر از 2 جواب دارند.
پس دامنه (∞,D = (-∞, -2) U (2 است.
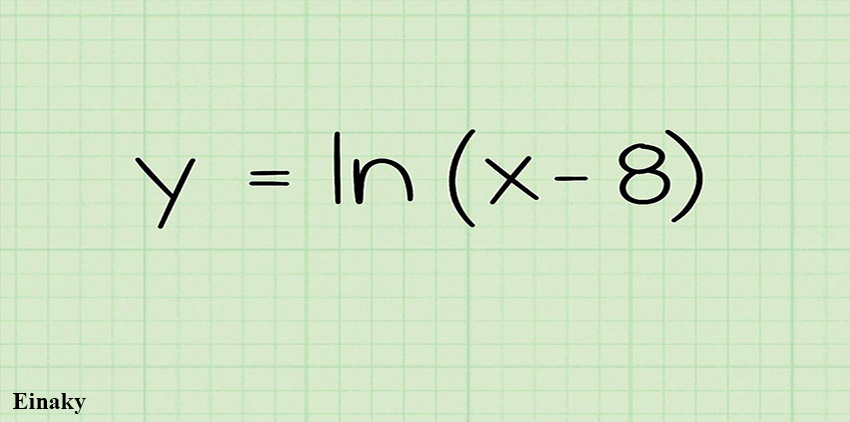
1- در این مثال می خواهیم دامنه تابع (f(x) = ln(x-8 را به دست بیاوریم.
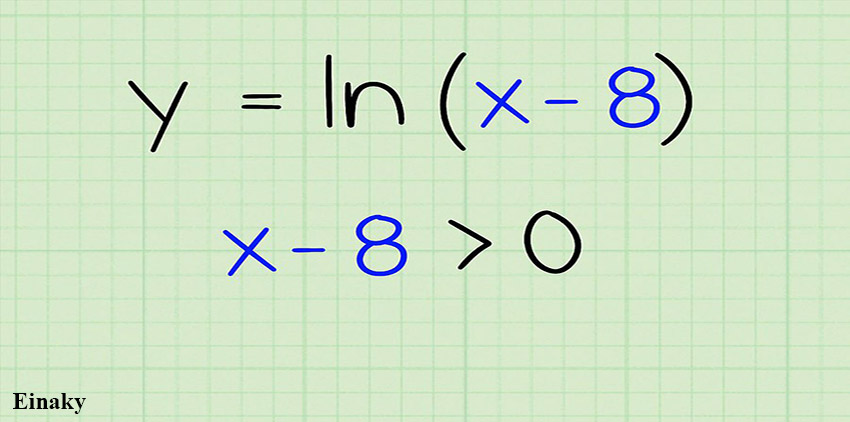
2- عبارت درون پرانتز را بزرگتر از 0 قرار میدهیم.
log باید یک عدد مثبت باشد،به همین دلیل باید عبارت بزرگتر از صفر باشد.
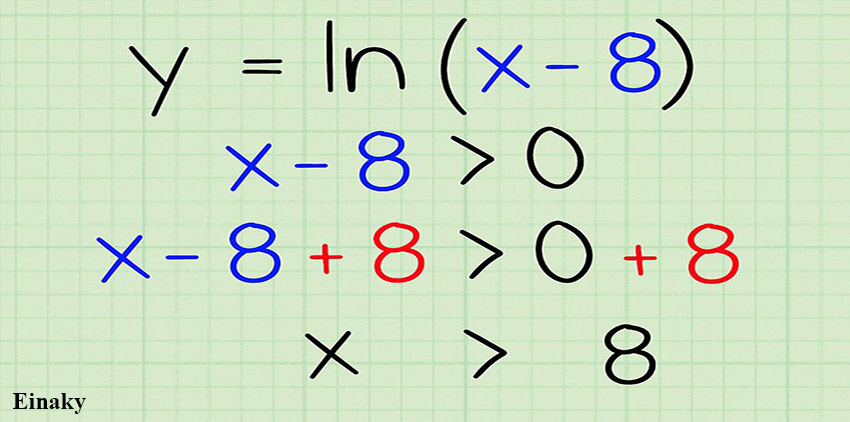
+8 را به هر دو طرف معادله اضافه کنید تا X به تنهایی در سمت چپ معادله قرار بگیرد.
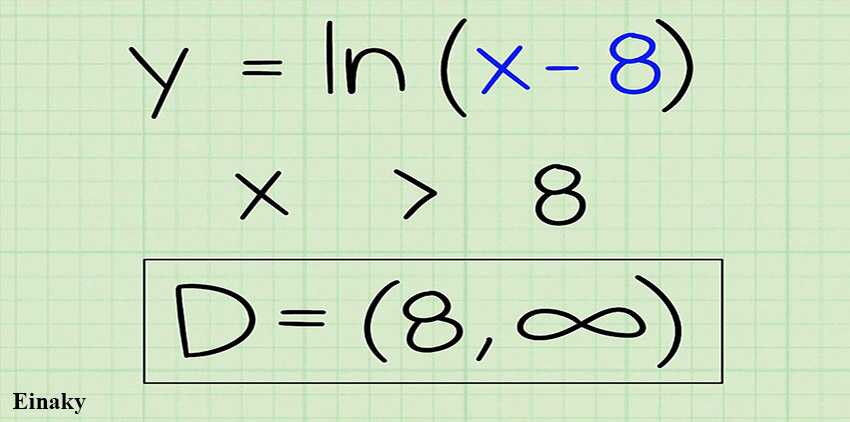
4- دامنه تابع لگاریتمی را بیان کنید.
دامنه این تابع برابر همه اعداد بزرگتر از 8 تا بی نهایت میباشد.
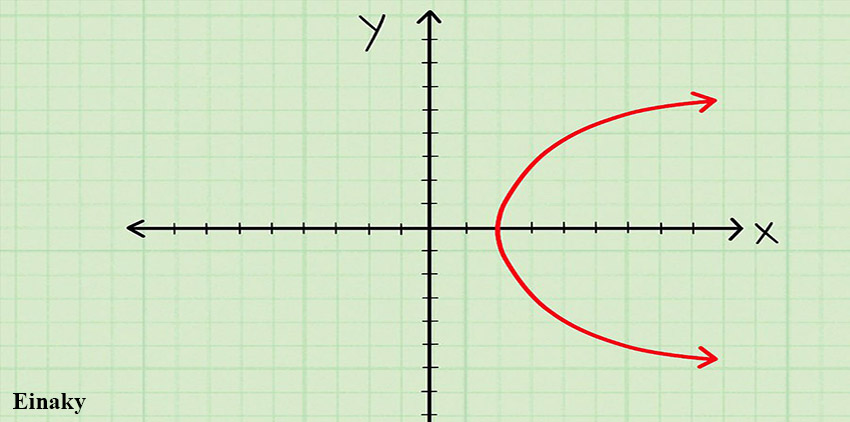
1- به نمودار دقت کنید.
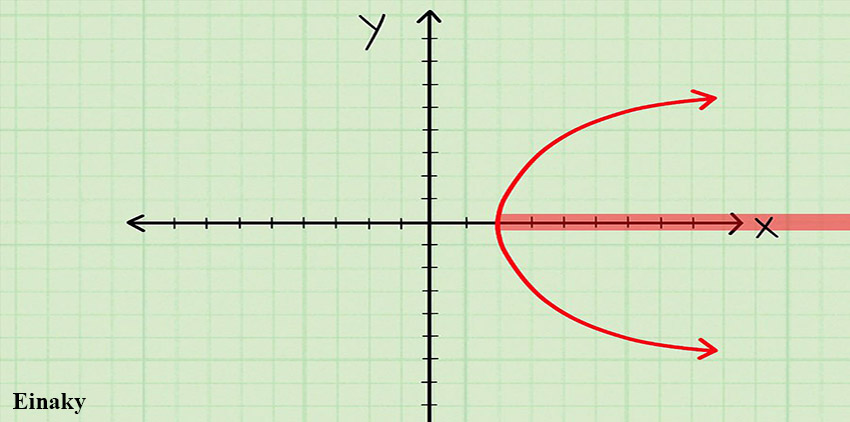
2- محدوده X هایی که درون نمودار قرار دارد را بررسی کنید.
البته باید چند نکته را در نظر داشته باشید.
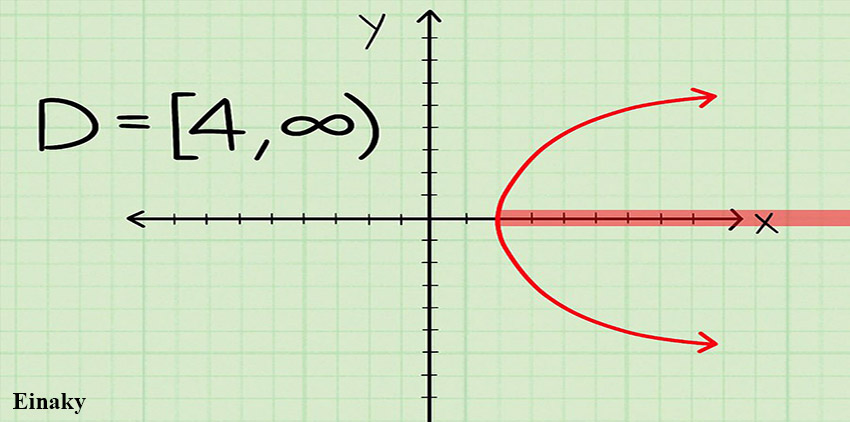
3- دامنه را بیان کنید.
بر اساس نوع نمودار دامنه را تعیین کنید.
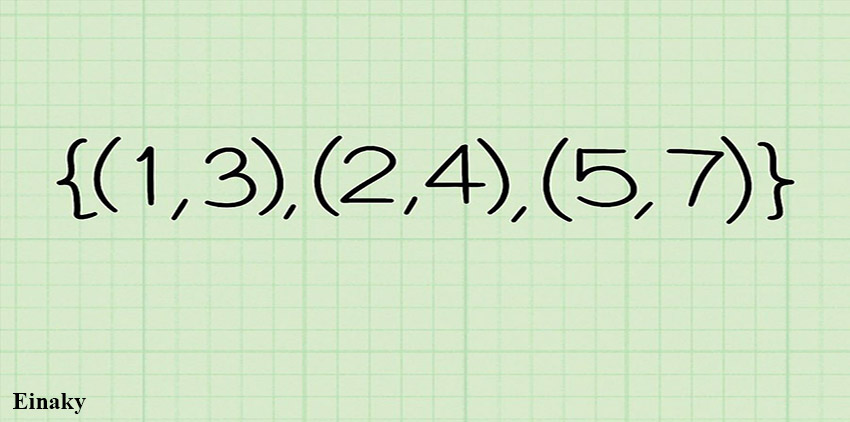
1- تابع زوج مرتبی {(1, 3), (2, 4), (5, 7)} را در نظر بگیرید.
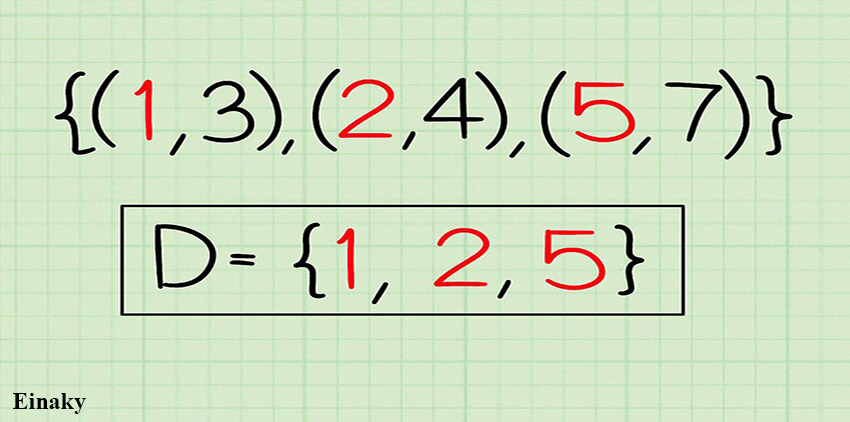
2- مولفه های اول زوج مرتب ها را بنویسید. 1,2,5
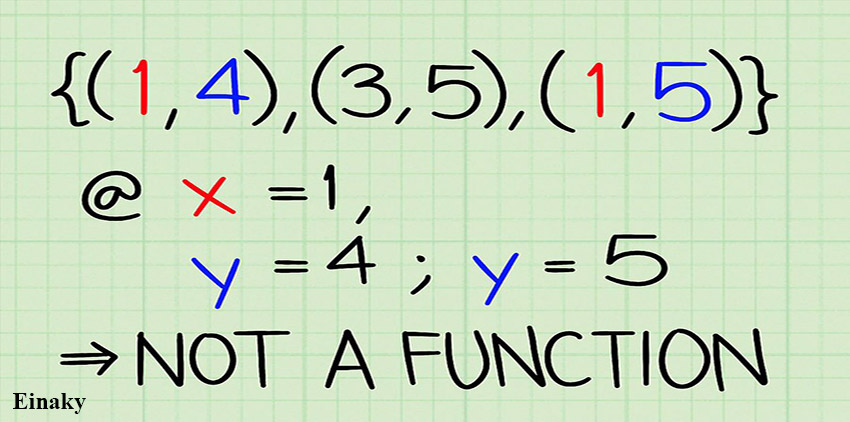
3- دامنه همان مولفه های اول زوج مرتب ها یعنی {D = {1, 2, 5 است.
4- مطمئن شوید رابطه داده شده یک تابع است.
یک رابطه زمانی تابع است که به ازای یک مقدار برای X یک مقدار برای Y به دست آید.
به عنوان مثال این رابطه {(4, 1),(5, 3),(5, 1)} تابع نیست زیرا به ازای مقدار 1 برای X دو مقدار برای Y به دست می آید.
حتما بخوانید: چگونه مجموع جملات دنباله حسابی را بدست آوریم؟
سلام و عرض خسته نباشید
خیلی سپاسگزارم از وقتی که صرف کردید برای خلاصه درس ❤️ خیلی مفید فایده بود .ممنونم
با احترام و سپاس فراوان از شما که از مطالب وبسایت عینکی استفاده کردی. امیدواریم که مطالب برای شما مفید بوده باشه. از اینکه وقت خود را صرف مطالعه مطالب مجموعه آموزشی عینکی کردید، سپاسگزاریم.
حتما کانال اپارات هم دنبال کن کلی فیلم آموزشی رایگان برات گذاشتیم
عالی
با احترام و سپاس فراوان از شما که از مطالب وبسایت عینکی استفاده کردی. امیدواریم که مطالب برای شما مفید بوده باشه. از اینکه وقت خود را صرف مطالعه مطالب مجموعه آموزشی عینکی کردید، سپاسگزاریم.
حتما کانال اپارات هم دنبال کن کلی فیلم آموزشی رایگان برات گذاشتیم
سلام ممنون خیلی به زبان ساده وروان توضیح دادید تشکر عالی👌👌👌
با احترام و سپاس فراوان از شما که از مطالب وبسایت عینکی استفاده کردی. امیدواریم که مطالب برای شما مفید بوده باشه. از اینکه وقت خود را صرف مطالعه مطالب مجموعه آموزشی عینکی کردید، سپاسگزاریم.
حتما کانال اپارات هم دنبال کن کلی فیلم آموزشی رایگان برات گذاشتیم
تشکر از مقاله ای که نوشتید برای بنده که از رشته انسانی به رشته مهندسی کامپیوتر کوچ کردم این مطالب بسیار ارزشمند هست
خوشحالم برات مفید بوده
مختصر و جامع بود متشکرم
خواهش میکنم زهرا جان
شما میتونی از روی سایت از فیلم های حل سوالات پر تکرار امتحانی هم استفاده کنی کافیه از منوی فیلم های اموزشی پایه خودتو انتخاب کنی
ممنونم واقعا از شما
خواهش میکنم
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
🥰کانال تلگرام عینکی
🥰گروه درسی عینکی در تلگرام
🥰کانال اپارات عینکی
سلام واقعا عالی بود🙏
خواهش میکنم فاطمه خانم
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
🥰کانال تلگرام عینکی
🥰گروه درسی عینکی در تلگرام
🥰کانال اپارات عینکی
عالی
عالی شمای
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
🥰کانال تلگرام عینکی
🥰گروه درسی عینکی در تلگرام
🥰کانال اپارات عینکی
عالی بود خیلی ممنونم واقعا مفید بود خیلی خوب یاد گرفتم
سلام خواهش میکنم
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
🥰کانال تلگرام عینکی
🥰گروه درسی عینکی در تلگرام
🥰کانال اپارات عینکی
خیلی ممنون عالی بود
عالی شمایی اقا مهدی
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
einaky_com
🥰کانال تلگرام عینکی
einaky_com
🥰گروه درسی عینکی در تلگرام
einaky_group
کانال اپارات عینکی
@einaky.com
عالی بوددد
ممنونم شادی خانمپپپیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
einaky_com
🥰کانال تلگرام عینکی
einaky_com
🥰گروه درسی عینکی در تلگرام
einaky_group
کانال اپارات عینکی
@einaky.com
واییییی ممنونممم خیلی خیلی مطلب خوبی بود من سال یازدهم ب خاطر این کرونا و تنبلی اصلا یاد نگرفتم و الان سال دوازدهم ب مشکل بر خوردم اما مطالب سایت شما رو ک خوندم دیگه میتونم دامنه توابع ب دست بیارم 😍😍❤👌🏻
خوشحالم که برات مفید بوده
پیشنهاد میکنم حتما در سایر شبکه های اجتماعی هم عضو بشی اونجا کلی آموزش های مفید و جالب داریم.
🥰اینستاگرام عینکی
einaky_com
🥰کانال تلگرام عینکی
einaky_com
🥰گروه درسی عینکی در تلگرام
einaky_group
کانال اپارات عینکی
@einaky.com
واقعا ممنونم واس این سایت بینظیرتون خیلی بهم کمک کرد 🌹
سلام Mahdiyeh عزیز
رضایت شما باعث افتخار ماست. ممنون از حضور گرمتون در سایت عینکی
خیلی عالی👌
جمع بندی کامل و مفیدی بود ممنون از زحماتتون❤
سلام خواهش میکنم.
ممنون از حضورتون در سایت عینکی
سلام ممنون از زحمتتون واقعا نتیجه داشت به بهترین شکل جمع بندی کردین که تو کوتاه ترین زمان شخص میتونه یاد بگیره بدون هیچ سر در گیجی
کاش کتابا هم به همین خوبی توضیح میدادن
خیلی ممنون از شما
سلام کامران عزیز
ممنون از نظرتون و خوشحالیم که سایت عینکی براتون مفید بوده.
سلام٬ واقعا چند وقته که دنبال یه منبع قوی برای بحث دامنه هام که مشکلاتمو حل کرد این سایت ٬٬ ممنون👏✌
ممنون سایت خوبی دارید
سلام
دامنه تابع 5√_1_3×√√
چیمیشع؟
ینی یه عبارت زیر یه دو رادیکال و یه عبارت زیر رادیکال بزرگ
سلام دقیقا متوجه سوال نشدم ولی در کل برای به دست آوردن دامنه توابع رادیکالی باید عبارت زیر رادیکال رو بزرگتر مساوی صفر قرار بدید
عالی بود مرررررسی از سایت عینکی
سلام خواهش میکنم .
دامنه این تابع رو میخام
Y=1/3x^2_8x+5/7
خود کتاب نوشته۲و۵ میشود دامنه..
اخه چرا ؟ میشه توصیح بدین ممنون
سلام وقت بخیر
این تابع یک تابع درجه دو هست
توابع خطی درجه دو و بالاتر توابع چند جمله ای حساب میشن
دامنه توابع چند جمله ای هم برابر با r یا اعداد حقیقی هستش
سلام
دامنه این تابع y = x + sqrt(x) + 1 چطور به دست میاد؟
سلام کافیه عبارت زیر رادکال رو بزگتر یا مساوی صفر قرار بدید دامنه تابع میشه (بینهایت,0] یعنی مجموعه اعداد حقیقی مثبت
سلام ممنون از سایت خوب عینکی
دامنه این تابع میشه چی؟
y = 3x + 8?
سلام این تابع چند جمله ای و دامنش میشه اعداد حقیقی
دامنه این تابع چطور به دست میاد؟
f(x) = 7/(x^2-1000)
کافیه مخرج کسر رو مخالف صفر قرار بدید x^2-1000
برای x دو مقدار – و + 10 به دست میاد که دامنه تابع میشه همه عددهای حقیقی منهای x = +-10
ببخشیدا.. ولی رادیکال 1000 جوابش 10 نمیشه.. 10 به توان 2 میشه 100.. وقتی X²_1000 رو مخالف صفر قرار میدیم.. یعنی میشه X² مخالف 1000.. رادیکال 1000 هم میشه حدود 31.. پس جواب میشه همه اعداد حقیقی بجز 31±.. البته ببخشیدا.. میدونم شما از من بلدترین
سلام اراد عزیز
ممنون که با دقت مطالب رو دنبال می کنی، به طور حتم ما هم عاری از اشتباه نیستیم و خیلی خیلی خوشحال میشیم که این نکات رو بیان می کنید.
مقدار رادیکال هزار توی کدوم بخش گفته شده؟ این متن مقدار رادیکال هزار رو مشاهده نکردم ممنون میشم دقیق تر بگی کدوم بخش این اشکال وجود داره که رفعش کنیم
سلام میخوام دامنه این تابع رو به دست بیارم میشه چی؟
f(x)=(x^2-5x+6)^(1/2)
عبارت زیر رادیگال رو بزگتر یا مساوی صفر قرار بدید می رسیم به این معادله x^2-5x+6>=0
از اتحاد جمله مشترک میتونید استفاده کنید و ریه های معادله رو به دست بیارید
دامنه میشه از منفی بی نهایت تا بازه بسته 2 اجتماعش با بازه بسته 3 تا مثبت بی نهایت
سلام به من برد داده شده و میخوام دامنه رو به دست بیارم چیکار کنم!!
سلام باید سوال رو ببینم توی بعضی از موارد باید مقدار برد رو توی معادله بذارید و مقدار X یا دامنه به دست بیاد